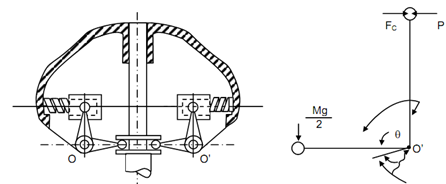
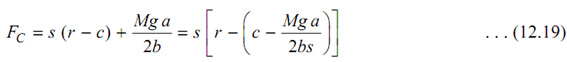Hartung Governor:

This governor also contains two bell-crank levers that contain fulcrum at O and O′. The springs oppose centrifugal force applying at the balls.

Figure (b) illustrated the free-body diagram of a bell-crank lever of Hartung governor illustrated in Figure (a) ball centre is r.

Assume s = Stiffness of the spring in N/m,

 P = spring force at radius 'r' in N,

 M = Mass at the sleeve in kg,

m = Mass of the ball in kg,

F_C = Centrifugal force (at the centre of the ball) in N,

c = Radius at which the spring force is zero, that means when the spring attains its free length,

a = Length of the arm to that the ball is linked,

b = Length of the arm connected to the sleeve, and

θ = Inclination of the arms illustrate in Figure (b).

(a)                                                    (b)

We will neglect the friction and the moment of the weight m_g around the pivot point O.

By taking moments of ball the external forces around O, we have the following

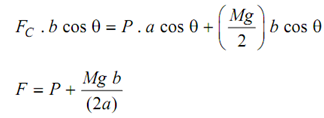
Furthermore, we see that P = k (r - c) as (r - c) is the compression of the spring.

Therefore,