Pascal’s triangle:
In simple cases of interacting nuclei, the relative intensities of the lines in a multiplet is given by the coefficients of the terms in the expansion of (1+ x)n. This can also be represented as Pascal's triangle shown in Figure.
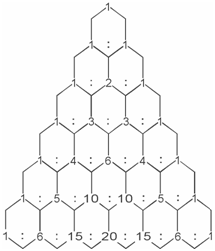
Figure: Pascal's triangle showing relative areas/intensities of split lines
The separation of these peaks in frequency units is called coupling constant. It is denoted by J and is a measure of the strength of the coupling interaction. The coupling constant is independent of the strength of the applied magnetic field.
These simple rules for determining the multiplicity of spin-spin interactions of adjacent groups hold only for cases where the separation of resonance lines of the interacting groups (?) is much larger than the coupling constant (J) of the groups (?>>J) . If ? ∼ J then the simple rules of multiplicity no longer hold good.