Tensor product surfaces:

The Bezier surfaces may also be illustrated in Tensor product form. If we arrange the control points into a matrix of m + 1 rows and n + 1 columns

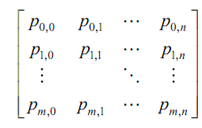
and the basic functions of the v-direction Bézier curve in a column matrix of n + 1 rows

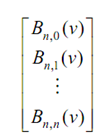
then the result of the parenthesis may be rewritten as a matrix product :

In this matrix form, the consequence is a column matrix of m + 1 entry. If further we make the basic functions of the u-direction Bézier curve in a row matrix of m + 1 entries :

                                                   [B_m,0 (u), B_m,1 (u),... , B_m,m (u)]

The equation of Bézier curve becomes the product of the three matrices as follows:

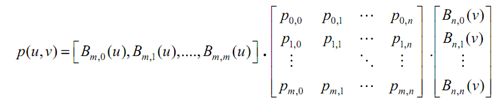
Thus, we have successfully converted the definition of a Bézier surface to a product form. As the entities of the control points matrix are matrices (that means each control point may be considered as a vector and therefore a matrix), it is the tensor product form in mathematics. As a consequence, Bézier surfaces are tensor product surfaces.