De Casteljau's Algorithm:

de Casteljau's algorithm may be extended to handle Bézier surfaces. More exactly, de Casteljau's algorithm may be applied many times to determine the corresponding point on a Bézier surface p(u, v) given (u, v).

Remember that the equation of a Bézier surface

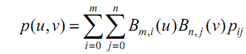
may be rewritten as

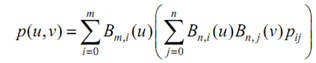
For i = 0, 1, ..., m, describe q_i (v) as follows :

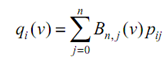
For a fixed v, we have m + 1 points q₀ (v), q₁ (v), . . . , q_m (v). Each q_i (v) is a point on the Bézier curve described by control points p_i0, p_i1, . . . , p_in. Plugging these back in the surface equation yields

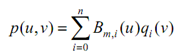
 It means p(u, v) is a point of the Bézier curve described by m + 1 control points q₀ (v), q₁ (v), . . . , q_m(v). Therefore, we have the following conclusion: To determine point p(u, v) on a Bézier surface, we may find m + 1 points q₀ (v), q₁ (v), . . . , q_m (v) and after that from these points determine p(u, v).