Optimal Provision of Public Goods:

The problem now is to determine how much of public good or bad should be provided. The standard approach in the case of private goods is to use price mechanism to allocate resources efficiently between different goods.  For public goods, however, we have seen that non-excludability invalidates the use of price mechanism for resource allocation. Samuelson Rule for the Provision of Public Good Consider an economy with two persons and two goods; one public good and the other private good. The amount of the public good is denoted by x, and the amount of the private good consumed by individual i be denoted by eel, i = 1, 2.  Note that because  the level of  consumption  of  the public  good must be  the same  for  each consumer, the argument x does not have  i  subscript. The technological possibilities of the economy are described by a transformation function T(x, y, +y₂).  The function T(.,.)  tells us how much of  the private good is  required to produce one unit of  the public good.

The welfare function  for  the economy  is  defined over the utilities  of both  individuals.  The welfare maximization problem can be written  as:  

where ul denotes  the utility level of individual  i. The  first order conditions  for the solution to  this  problem are:

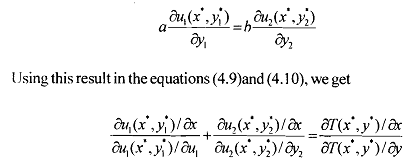
'The  above  is a classic optimality condition  for a public good first derived  by Samauelson  (1954). According to the Samuelson rule, the social value of a good is equivalent to the combined willingness to pay of all the consumers of that good. Note that the conditions for optimality for a public good differ from the conditions characterizing a competitive market solution.  At the optimal level of  the public good, instead  of MRS=MRT  for each consumer, we require  sum of marginal  rates of substitution between public and private goods across all consumers be set equal to the marginal rate of  transformation. The MRS,  can be interpreted as individualized prices -how much consumer i is willing to sacrifice of the private good to pay for one more unit of the public good. This can be thought of as  how much consumer i should be taxed. Under this interpretation we see  the basic "duality" between public and private goods: in the private-goods case, we all consume different amounts of the good but pay the same price; in the public good case, we all consume  the same amount of good but have different prices.

Samuelson condition  for  optimal provision of a public good: The marginal rule of transformation  of a public good-for a private good should be equal to the sum over all individuals of their individual marginal rates of substitution of  the public good-for the private good.