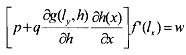Non-optimality of the Competitive Outcome:

The question arises why should we be worried about externalities? The  basic problem is that the generator of the externality is deciding how much of the externality to produce but is not taking  into account the effects  of  the externality on others. Let us model  

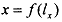
such interactions  in a  simple way. Suppose we have two producing units, a steel mill and a fishery along  a  river, steel mill being upstream.  The  steel mill produces  x units of steel from labor according  to a production function where I, denotes amount  of  labor employed in steel mill. In contrast wi  th the standard competitive model, however, we assume that each unit of steel production unavoidably produces some waste or pollution, which is dumped into the river. Let h(x), h'(.)>O, represent this pollution (pollution  is monotonically increasing in steel production). The fishery produces  y units of fish depending on  the amount of labor it employs and the amount of pollution in the water

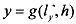
We assume f(.) and g(.,.)  to be concave production functions and [/]<0. As the steel firm's production ofh(.)  affects the fishery's output, it generates an externality. Let p, q, and w denote  the prices of steel,  fish and  labor, respectively. We assume  perfect competition  in factor and product markets so that  the actions of either the steel mill or the fishery do not affect these prices. The profit functions of the two firms are given by

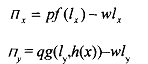
Each of the two firms chooses output and thus the amount of labor employed to maximize its profit. Assuming interior solutions,  the necessary and sufficient first order profit maximizing conditions are

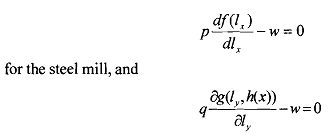
for the fishery. These equations imply  that the two firms will employ  labor until the value of marginal product of labor in their respective units is equal  to the wage rate. The output chosen  by the two units may not be socially  efficient as  the output of the steel mill adversely affects the output of fish but the effect is being ignored by  the steel producer. We will see below  that she  is producing  "too much" steel. What would a socially efficient production plan look like?

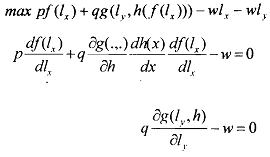
In any Pareto optimal allocation, the optimal level of h must maximize thejoinl surplus of  the two firms. Let us, therefore, consider what would happen if one  tirm owned both the steel mill and the fishery, and maximized aggregate profits: