Determination of optimal allocation:

The determination of the optimal allocation of a private and apublic  good is illustrated geometrically in Fig. while that for  a public good is given at Fig. The horizontal axis  shows the  quantity and the vertical axis shows price, marginal rate of substitution and marginal  rate of transformation.  Individual marginal rates of substitution are represented by MRS,  i = 1.2. curves.  In Fig, the curve to the extreme right, MRSH represents aggregate marginal  rate of  substitution  and  is obtained by summing  individual MRS, curves  horizontally. For any given price, we see the  total amount of  the good  the consumers wish  to consume. The condition  for Pareto efficiency  in the case of private goods  is  that each agent  is consuming at a level ,where her MRS,  equals the price ratio.

which in turn is equal to the MRT. In order to determine price, we find the point of intersection of AIRSH  curve and the MRT curve. Once we know the price, p: we can find  the  consumption levels  ofeach  agent  by looking  at  the consumption  levels that equate MRS, with pi for each i. In Fig. y =  y₁ +  y₂ is the total output of the private good, y: being  the amount consumed by consumer i.

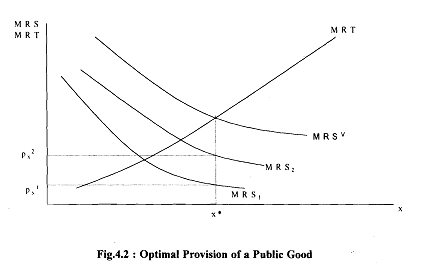
In the case of a public good, we proceed differently . We are  interested in the  total marginal willingness  to pay for specific  amounts of  the public good. The difference here is  that both consumers consume  the same amount of the good. The condition for Pareto efficiency in this case is that the level of consumption of the public good is where  the sum of the  individual marginal  rate of substitution  for both consumers equals the MRT, i.e.,  the total willingness to pay equals  the social cost.

To capture this, we sum individual MRS, curves vertically. The aggregate curve is shown as MRSV The point of intersection of the MRT  curve and the MRSV gives us the optimal level of output of the public good. We can find each agent's willingness to pay at  that level of output by inspecting  the individual MRS  curves. We could use this information  to tax the individual consumers  in order  to pay for the public good.

Then each agent would be paying exactly his or her true valuation of the public good. This kind of taxation scheme - called a Lindahl equilibrium - seems to be an especially fair way of paying for the public good. In Fig,  pi.  i = 1,2 represent these individualized prices. This kind of pricing scheme  could be rather difficult  to implement.