Simultaneous move games with mixed strategies:

To  review, a  pure  strategy specifies a non-random  plan of action for a player. In other words, there  is no probability attached  to the choice  of  strategy.  In  contrast, a mixed strategy specifies that an actual move be chosen randomly from a set of pure strategies with  some specific probabilities. The most  important aspect of mixed strategy from our perspective is that under very general conditions, every simultaneous game has at least one Nash equilibrium in mixed strategy. Consider Example  9, where we  showed  that  there does  not  exist any  pure strategy Nash equilibrium. But we will show how  the situation changes  if we introduce  some  randomness  in  the  process  of  picking  up  the strategies. Suppose player  1 mixes her strategies by probability p and  (I-p), i.e.,  she can choose strategy S1  with probability p and S₂  with probability (1-p). And player 2  mixes  her  strategies  with probability  q and  (1-q)  respectively  with [0≤p≤1;0≤q≤l].

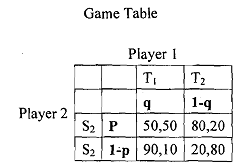
Since there  is  randomness  in  picking up strategies,  the  payoffs  are no more certain and are now expected payoff  (expectation of a random variable taking the  valuesx,,x,,x,  ......xn with probabilities  p,,  p,, p3  ..--.-p, is  given  by

Player 1 will choose p  in  such a way  that  E₁ is maximised and  player  2 will choose q in  such a way that E₂ is maximised.

If we  look at the final expression of E₁,  player  1 can do nothing about the non- shaded part  of  the  expression  El,  as her  choice variable p does  not  appear there, but she can affect the shaded part of El. If (6 -  10q) is positive she will choose p=l, if it  is negative chooses p=O  and-if  (6 - 10q) is equal to zero,  she will  be  indifferent  about  her  choice  of  p.  This  gives  the  best response correspondence of player 1. We put it more formally as,

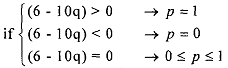
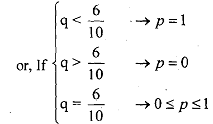
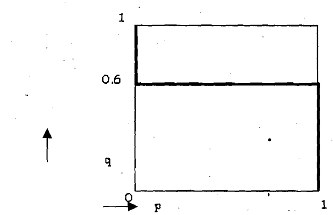
We  can  plot  the  best  response correspondence of  playerl,  on  p,  q  space as follows

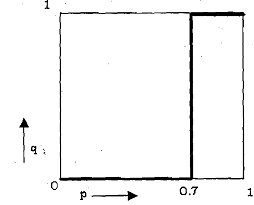
Similarly, we can derive the best response curve of the player 2, which  is

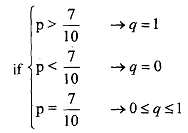
We can plot the best response curve of player 2 in a similar way

If we  plot  the two best  response correspondence  together in a single diagram, they will intersect at a point,  say E.  The coordinate of  this point  (p=0.7 and q=0.6) gives the mixed strategy Nash equilibrium of the game. In equilibrium, player 1 mixes her strategy S₁  and S₂ with probability 0.7

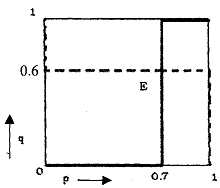
and 0.3 respectively; and  player  2  mixes her  strategy  T_I  and  T_I with probability 0.6 and 0.4, respectively.