Pure strategies:

In  all the game we  have studied so far, each player had only a finite number of pure  strategies at her disposal. But consider the games  in which  the player  is choosing price, quantity or expenditure or to be  specific a variable, which is continuous  in  nature.  In  this section,  we  will  discuss  how  to find  Nash equilibrium in  such games.

The method we will employ  to  find the Nash  equilibrium  in  such  games  is known  as the  "best  response analysis".  We  know  that  in  equilibrium,  each player's strategy must represent her best  response to that of her rival.  In  case pure strategies, which are continuous  in nature, we can plot the best responses of a player  against the possible strategies of the other player. This will  be  a continuous curve as the strategy space of the other player  is also continuous (we ignore  the case where the strategy space of  the  other player could  be discrete).  This  is  known  as  the  "best  response  curve"  or  the  "reaction function". Nash  equilibrium  is  the  combination of strategies where the two best response curves intersect in the strategy space.
We will  illustrate  the above method by  solving  the Coumot model of duopoly.

Let ql  and q~  be  the quantities of a homogeneous product produced by  firms  1 and  2,  respectively. We assume a simple demand curve, P (Q)= a -  q, which gives the market clearing price when aggregate quantity in  the market  is (ql + q?  1. To be more precise,  

Let us assume that the cost of producing quantity q, for the i"  firm is given by C,  (q,) = c. q,,  which  implies that there  is no fixed cost of production and the marginal cost of production is c, which  is constant at c. We further assume a > c,  Following Cournot, firms simultaneously choose the quantity of output they will produce and their payoff function  is their profit.

In  order to find the  Nash  equilibrium of the game  we  first translate the problem  in  to  a normal  form  game. Recall  from previous unit that  a normal form game must specify,

i)  players of the game

ii)  strategies available to each player

iii)  payoffs received by  each player after strategic interaction.

There are 2 players in this game firm  1 and  firm 2.

The strategies available to them  is  a continuous variable,  it  is the quantity  it might be  produced. We assume that quantities are continuously divisible  (we trivially exclude negative output). Thus, the strategy space of each player  is Si -  [0, a),  which  is non-negative real numbers,  in which case a typical strategy s,  is a quantity choice, q,  2 0.

As we have defined earlier,  the payoff of the firms  is the profit, which given by

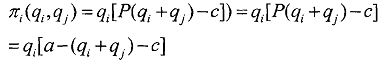
The strategy pair (q*,, q*$  is a Nash equilibrium if for every player q*,  (i=1,2) must solve the optimisation problem,

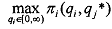
The  first order condition for firm  i's  optimisation problem  is both necessary and sufficient. It yields,

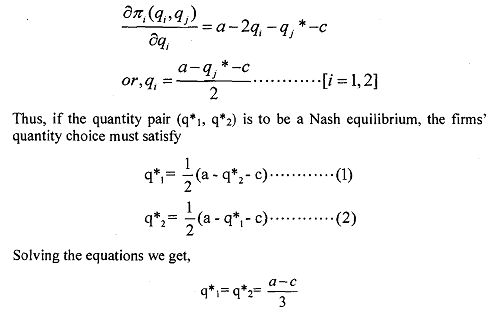
Equation 1 gives the best  response curve of firm  1  and equation 2 gives the best response curve of firm  2. They intersect at

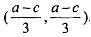(Try  to  solve the game graphically)