NASH EQUILIBRIUM:

The purpose of tabular representation  of a simultaneous move game  is  to predict  the actual behaviour  of the  players and  the resultant payoff when  the game  is played. We look  for an equilibrium  in which each player's action is the best  response to the actions of the other players. The equilibrium  concept we employ here  is known as  the Nash equilibrium. The concept is named after mathematician and economist and Nobel Prize winner  John  Nash. Nash described the equilibrium  of  a  non-cooperative game  as a  configuration  of strategies, one for each player such that each player's strategy is best for her given that all the other players are playing their equilibrium strategy.

Definition:  In  a  'n'  player normal form game G={S₁, S₂,...  S_n;  U₁,  u₂,  ...  u_n},  the strategies  (s₁*,  s₂*,  .......,  s_n*,) constitute a Nash equilibrium if, for each player  i, s,  is player  i's  best  response  to the  strategies specified for  the  (n-I) other  

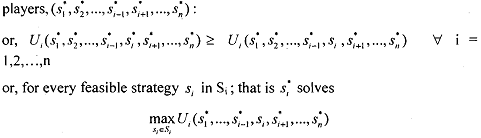
Nash  equilibrium  is  strategically stable and self-enforcing because  no  single player wants to deviate from her predicted strategy.

Example: Game of Prisoners' Dilemma

This  is a classic example  in  game theory. Two prisoners have  two strategies available to them: confess and not confess. They are kept  in two separate cells and the payoff  to  the  player when  a  particular pair  of  strategy  is  chosen  is given  in  the  following payoff matrix.  The  negative numbers  in  each  celI represent years of  imprisonment. By  convention  the  payoff to the  row player is the first payoff given  in each cell.

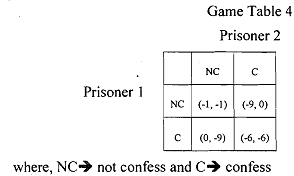
Note  that  irrespective  of  what  prisoner  1  chooses,  prisoner  2  will  always choose  'C'  to minimise  her years of  imprisonment. Similarly, prisoner1 will always  choose 'C'.  Therefore, (C,  C)  is  the Nash equilibrium  of  the  game (though  it  seems  that  (NC, NC)  is  the  likely  equilibrium,  but  it  is not Nash equilibrium).

In  the above example,  there was a unique Nash equilibrium of the game. But there may be  cases  in  which  there are  multiple Nash  equilibria  in  a single game. Let us illustrate with the famous game of battle of sexes.