Minimax strategy:

As  many  simultaneous move  games will  not  have dominant  strategies, we need  to  formulate  some other technique  to solve  such games.  We  are  still looking  for a Nash  equilibrium  in  which  every player  does the  best  she can, given the action of  the other players. One  logical approach  to  solve a  zero-sum  game with  no dominance  involves the  idea of minimax. Due  to the  inevitable nature  of zero  sum  game as each player  tries  to  maximise  her  payoff,  she  inevitably  minimises her rival's payoffs. Let us consider the following payoff  table (a shorthand  notation  of a hypothetical  zero  sum game  in  which  the payoffs of  the  row player  are only shown).  

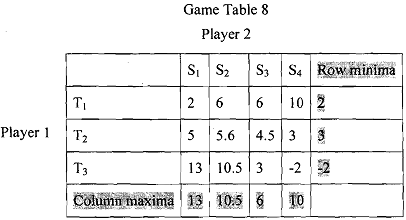
Player1 will  try  to maximise  the  payoffs given  in  the table  by  appropriately choosing her strategy, whereas player 2 will  try minimise the payoffs  given  in the table by  appropriately choosing her strategy as her payoffs are negative of the payoffs given  in  the table. Therefore,  player  1  will  choose  the  strategy which  gives her the  highest among the  row minimum  or  the  maximum  among  me  minimum.  This technique of finding  the best  strategy  for  the  row player  is called "maximin" in short.

Similarly, player 2 will figure out the highest payoffs  in  each column,  i.e.,  for every  strategy of  her.  These are  called  the  column maxima.  Then she  will choose that  strategy which  corresponds  to  the  lowest  among  these  highest payoffs. This  technique is known as "maximin"  in short.

Thus,  player1 will choose  T₂ and player  2 will  choose  Sg. The  payoffs that will accrue to  the players1 and 2 are 4.5 and -  4.5, respectively. Always  remember  that "maximin" and "minimax"  methods are applicable  to the zero  sum  games only. The method  may fail when  applied  to a non-zero sum  game.  In  such  games choosing the  strategy that makes ones' minimum payoff  as  large as possible may not be ones'  best  strategy because  in  a non- zero  sum  game  the  opponent's worst  need  not  be  ones'  best,  so  there  is  in general  no  reason  to  believe that  one's  opponent  is  out to make  someone's payoff as low as possible without looking at her own payoff.