Iterated elimination of strictly dominated strategies:

For  obvious reasons, no rational  player will  play  strictly dominated strategy (as  dominated  strategies  render less  payoff whatever  be  the  opponents strategy). This idea can be  used to  find  the solution of a game. Consider the following example:  

Example:

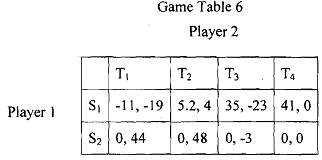
Player 1: Neither S₁  nor S₂  is strictly dominant.

Player 2: T₂  strictly dominant strategy (check it out yourself).

Therefore, player 2 will play T₂  only, and hence the game table reduces to the unshaded region of Game Table

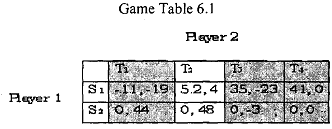
Now,  in  the  reduced game table for player  S₁ is  the strictly dominating strategy. Therefore,  player1 will  choose  S₁.  So, the solution of the game  is (S₁,  T₂).

From  a  game  table,  we  can  reach  the  solution  by  eliminating the strictly dominated  strategies. This process of obtaining solution of a game  is known as called iterated elimination of strictly dominated strategies (IESDS).

Although  the process  is  based  on  the appealing idea that rational players do not play strictly dominated strategies, it has two drawbacks, viz.,

i)  in each step each player assumes that the other player is rational. That is, we  need  to assume that not only players are rational, but they also know that all players are rational and their rivals also know that she knows that she  is  rational,  and  so  on  ad  infinitum. This chain of information  is known  as  common knowledge. Therefore,  we need  to assume that players are rational and rationality is common knowledge;

ii)  there  could  be  situations  in  which no  strategy  is  strictly dominated. Tn that case, we  cannot apply IESDS to  reach  the solution.