DOMINANT STRATEGIES:

A  player  in  a  simultaneous move game may have any finite number of pure strategies at her disposal. We call one of these strategies her dominant strategy if  it  outperforms  all  of her  other strategies, no matter what  any other  player does.  In  Example  3,  the  strategy  'c'  for each player dominates  the other strategy  'NC',  since it gives higher payoff no matter what other players do.

Definition:  In  the normal form game G={S₁,  S₂,...  S_n;  U₁, u₂, .  .u_n),  let  s,'  and  s," be feasible strategies  for the  player  I  (i.e.,  s,'  and  s,"  are members  of  S, ). Strategy  s," strictly dominates strategy  s,'  ,  if for each possible combination of other players' strategies,  i's  payoff from  playing  s,'  is  strictly  less  than  i's payoff from playing  s:'  . Symbolically,  

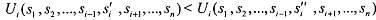
for  each (s₁  ,  s₂ ,...,  s_t-1,  ,  s_t+1,  ...,  s_n) that  can  be  constructed  from  other  players' strategy  spaces (S₁,  S₂,...  S_n) . Strategy  s,"  is  called strictly dominant strategy for player  i.  The dominance  is  said  to be weak when there is a weak inequality  (≤  rather than <) in the above inequality.