Cell-by-cell inspection:

There  is an alternative to all of the solution methods  considered so far in  this unit. 'Chis alternative  is known as the cell-by-cell inspection. This method  can be  applied  to  find  the Nash equilibrium (equilibria) of any zero or non-zero sum  game.  This method is  not sophisticated  but  some one  can be  sure  of finding all  the Nash  equilibria of a game following this method, which  other methods might overlook.

The  easiest way  to  verify that a player  is using her best  response  is just  to check, at a particular  outcome, whether she would want  to change her choice of  strategy.  If she  would, then  the  strategy she  is  using  cannot  be  her best response to  the strategy (ies) chosen  by  her  rival(s).  If she would not want  to change, and  if no other player would want to change either, then we must be sure that the outcome we are considering must be a Nash equilibri.um. Consider the following hypothetical game table:  

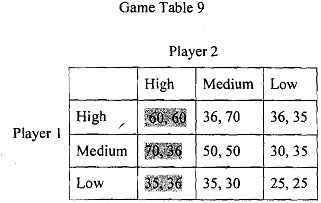
Let  us  begin with  the cell  in  the  upper  left  hand  corner  of the  table (High, High). We need  to check whether this outcome constitutes Nash equilibrium or not. To do this, we simply assume that Player 2 is playing her equilibrium strategy  (High).  Then  we  investigate whether there  is  any incentive for player  to  deviate  from  High and  look  at  the  shaded column. Given  that
Player 2  is playing High as her equilibrium  strategy,  there  is an incentive for player 2  to adopt "Medium"  instead of "High"  which  fetches her  10 units of extra payoff  (70 - 60). Therefore, we can conclude that (High, High) does not constitute Nash  equilibrium. Next we  consider  the  strategy (Medium, High).

In  this case, given player 2 is playing  "High"; player 1 is optimally playing "Medium".  But given  the  fact  that player is playing  "Medium",  Player 2  is not  playing  her  best.  She  would  have  done  better had  she  been playing "Medium"  too. This would have fetched her  14 (50 - 36) units of extra payoff. Therefore, (Medium, high) cannot be a Nash equilibrium.

Thus, in solving a game following the method of cell-by-cell inspection, we need  to check every possible combination of  strategies, whether or not  they serve as a Nash  equilibrium. Generally, we  keep strategy of one player fixed and check whether the other is playing her best. If she does so, then we  fix her strategy  and  check whether the other  is  playing  her  best. If  both  these conditions are satisfied, then we  say that there  is no  incentive for the players to deviate fiom that strategy, and they constitute Nash equilibrium.