Theory of Second Best:

Government takes steps to make this market competitive,  it would appear that social welfare would increase  (as price and marginal cost will  be  equated  in this market) irrespective of whether in some other markets competition cannot be  enforced and  therefore  in  them  Pareto  optimality  conditions cannot  be satisfied. The second best theory holds that, this will not  lead to the increase  in social welfare. In other words, the second best solution is not desirable. Although a fonnal proof of the theory of second best is bit complicated, it can be represented graphically in  the Figure below.  

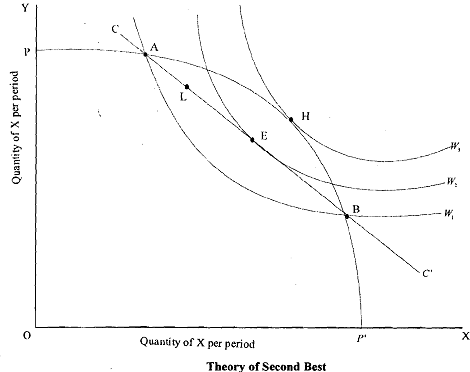
In the Figure, PP'  is the production possibility curve and all points on the curve are Pareto efficient. According to Lipsey and Lancaster, it is sometimes better to move inside PP' to achieve a higher level of social welfare in case all marginal  conditions are not satisfied. To demonstrate  this,  social  welfare curves or  community indifference  curves are  drawn  in  the figure like individual indifference  curves.  These  social  welfare  curves  represent combinations of two products X and Y, which yield  the  same level of social welfare. Further, the higher the level of social welfare curve denotes higher level of welfare.  It will be  seen from the  figure that point Hat which  social welfare curve  is  tangent to  PP' shows  maximum  social  welfare point satisfying  all the marginal conditions of Pareto optimality. Now,  suppose due to the existence of monopoly  in  the markets of the  two goods, X  and Y,  the socially  best  point  H  is  unattainable. Further, suppose that under  such circumstances,  combinations lying on the  line CC'  are attainable. Suppose the economy  is  at  present at point  L  on  the  attainable line  CC'.  If Pareto optimality is to be achieved, we can move from a point L, which  is inside PP' to point A or B which are also on the attainable line CC'. However, as will be seen from the figure, moving to point A or B on PP'  would put us  in  a  lower welfare curve W1  If  instead  from point  L, we move  the  point  E, which  is inside PP'  and is  therefore Pareto  inefficient  and  yields a  higher level  of welfare as indicated by Wz. Thus, the theory of second best asserts that when one  of  the marginal  conditions of Pareto optimality  is  not satisfied due  tosome or other reasons, it may be better to violate other marginal conditions of Pareto optimality  to achieve maximum possible social welfare.

The theory of second best  has  been  applied to question, the desirability  of advocating competitive pricing  in some particular markets when  it  is known that Pareto conditions do not hold in other markets. However, the advocates of such policies in making some markets more competitive in  achieving Pareto optimality argue that  as the markets  in  question  are  unrelated,  it  does not matter for attaining maximum social welfare that  in  other market conditions for Pareto efficiency are not fulfilled. Advocates of the latter policy argue that when markets are  relatively independent or unrelated, marginal cost pricing increase social welfare. Thus,  in  the words of Prof.  S. Charles Maurice and Own.  R.  Phillips,  "the  theoy  of  second  best  applies  most  strongly  when
markets are closely related: that is, they either produce  cornplementa  y goods like bread and butter, or one market  is an intermediate supplier of another as in  the case of tyre makers supplying automobile producers".