Bergson Samuelson:
The Bergson-Samuelson SWF shows that, given the set of Pareto-optimal points, which is' more desirable from "society's" point of view, where the notion of social desirability was subsumed in a social welfare function.
Heuristically, we can envisage the upper contour set of the SWF as a set of "social indifference curves" in utilities space, as shown in Figure.
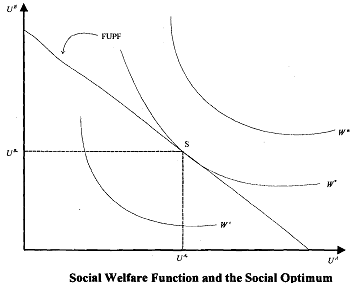
According to Bergson, there are some desirable properties of a society which are captured by the SWF: for instance, social welfare increases if the utility of any of its members increase and none decrease (the "Pareto principle") that yields northeasterly ascendance of the social indifference curves. It is worth mentioning that the consideration of fairness and equity are incorporated into the SWF and are reflected in the shapes of social indifference curves. In other words, it can be argued that equity is socially desirable; consequently, extreme distributions of utility ought to be given less weight. Thus, the convexity of the social indifference curve needs to be accepted and like the usual indifference curves they are also non-intersecting.
By superimposing social indifference curves on the GUPF as in Figure, we can see that allocation S = (uA*, uB*) is the point on the GUPF that attains the highest social indifference curve, and maximises the social welfare function, yielding social welfare index W*. Thus, the "social optimum" is determined by the tangency of the social indifference curves and the GUPF. The SWF as depicted in Figure can be explained by the following functional form:
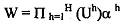
where ah are the weights assigned to each household in the social welfare function. Such a function yields the convex social indifference curves in Figure and is sometimes called a "Bernoulli-Nash" social welfare function.
It is to be noted that the slope of the social indifference curves is equal to the negative of . This last term in the expression is the "marginal rate of social substitution" between consumers A and B, or MRSSAB. Now, we know that the slope of the GUPF will be merely the ratios of the marginal utilities of income of households A and B, thus the tangency
condition is that:
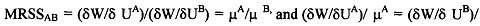
or the social marginal utility for each household is equal across households. We can extend this explanation to analyse some alternative welfare function as mentioned above. As per the classical or Benthamite or "utilitarian" social welfare function, the SWF can be constructed as a linear sum of weighted utilities, e.g;
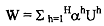
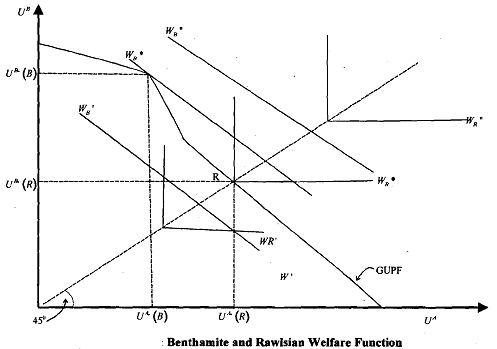
which is a direct sum. Thus, as stipulated by Jeremy Bentham and the Utilitarians, this one maximises the (weighted) sum of individual utilities and yields linear social indifference curves (WB', WB*, WB'') as shown in Figure below.
Bergson-Samuelson SWF states the conditions for "social justice", as that, 'the marginal rate of social substitution between households A and B is equal to the ratio of marginal rates of substitution of A and B. In other words, this implies that the allocation of goods is done in such a manner so as to have the utility distribution compatible with the "worthiness" of the individuals according to the social welfare function.