As the change in slope from end B to A is θ_A, it is equal to the area of M/EI diagram between these points

i.e.  θ_A =   M_A/EI .a/2 -M_B/EI ((L-a)/2)

Also the intercept on the tangent at B made by the vertical through A is equal to the moment of M/EI diagram about A. Since the tangent at B passes by A, so this intercept is zero, hence,

(M_A/EI.a/2)(a/3)-(M_B/EI(L-a)/2)(a+2(L-a)/3))=0

Also we know from similar triangles that a/L-a = M_A/M_B                                        

From Eq. (3.3),

M_A. a² = M_B (L - a) [3a + a² - 2 (L - a)]

Dividing by (L - a)² we have

M_A(a/L-a)² =M_B[3(a/L-a)+2]

On Substituting Eq. (3.4), we get

M_A/M_B (M_A/M_B)² =3(M_A/M_B) +2

If M_A/M_B = r this gives r³ = 3r + 2 or r3 - 3r - 2 = 0

Giving (r + 1)² (r - 2) = 0 hence r + 1 = 0 or r - 2 = 0

As the ratio r = M_A/M_B = - 1 is not acceptable since M_A = - M_B gives the case of a uniform sagging moment all over the beam, thus,

∴          M_A/M_B =2 or M_A  =2M_B                                                                                                       

Also a/L-a =M_A/M_B =2 or a 2L/3

Substituting Eqs. (3.5) and (3.6) in Eq. (3.2), we get

M_A = 4EI θA /L

and     ∴ M_B= M_A/2 =2EI θA /L

Thus, a rotation of θA at hinged end A is produced by a moment  4EI θA /L at the end A, while at the fixed end B the moment induced is half of this, i.e. 2 EI θA/L and both are clockwise if θA is clockwise.

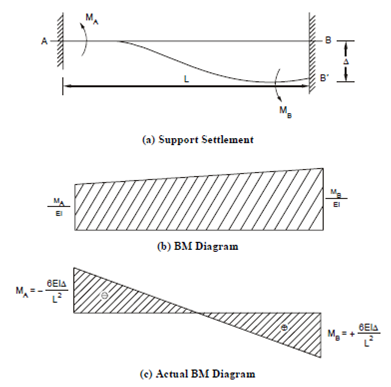
Next, let us compute the fixed end moments due to a support settlement or end deflection as shown in Figure 6(a).

Figure