Representation of Harmonic Quantities of Rotating Vectors

The stable state vibration of a spring mass system illustrated in Figure 1 is given by

Equation (3) that is as follows:

                   x = X sin (ωt - φ)

This vibration tale place under the effect of a harmonic exciting force F_o sin ωt. The velocity and acceleration of the mass are specified by

 x'= X ω cos (wt - φ) = X ω sin (ω t + (π/2) - φ)

and

  x''= - X w²  sin (wt - φ) = X w sin {wt + π- φ}

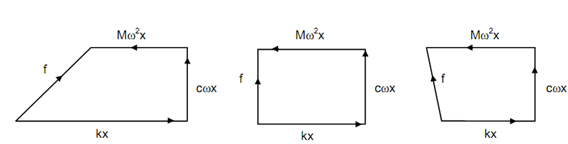
A harmonic function of time may be conveniently represented by a rotating vector as illustrated in Figure 3. All of these vectors are rotating vectors and angular speed of rotation is ω, the frequency of the force. The spring mass system residue under dynamic equilibrium under the activity of spring force, inertia force, damping force and external force F. Figure 4 indicates the force diagrams for three conditions:

(i)  ω / ω_n < 1 ,

(ii) ω/ ω_n  = 1 , and

(iii) ω/ ω_n > 1 .

Figure 1

 These forces make force polygons. For ω/ ωn  < 1 , inertia force is less than the spring force.

For ω / ω_n = 1 , inertia force is equivalent to the spring force. For ω / ω_n > 1 , the inertia force is greater than spring force.

              (i)                                                             (ii)                                                                (iii)

        Figure 2