Frequency Ratio Corresponding to the Maximum Amplitude:

The steady state amplitude is specified by following

                  X = DM × x_st

Hence, X will be maximum if DM is maximum. As

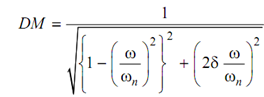
DM shall be maximum if denominator is minimum, that means

f (r ) = {(1 - r ² )²  + 4δ²  r ² }        is minimum.

Here      r =  ω /ω_n

d f (r) / dr = f (r ) = {2 (1 - r ² )} × (- 2r) + 4δ²   × 2r = 0

or            - (1 - r ² ) + 2δ²  = 0

or            r ² = 1 - 2δ²

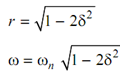
Since damping enhance the frequency for maximum amplitude drop. The maximum amplitude is given by

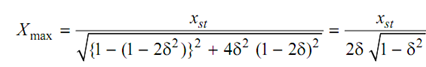
 While amplitude at the resonance

X _resonance  =  1/2δ    

While damping is very little both are closely same.