Find the maximum stress in the shaft:

A disc of mass 4 kg is mounted on a shaft having 10 mm diameter at the centre among the two small bearings. The span length is equivalent to 50 cm. The eccentricity of mass is equivalent to 2 mm from the geometric centre of the disc. The corresponding viscous damping at the point of disc mounting is equal to 50 N sec/m. The angular speed of the shaft is equal to 250 rpm. Find the following :

 (i) the maximum stress in the shaft, and

(ii) the power needed to derive shaft. Let E = 2.0 × 1011 Pa.

Solution

It is given that

Mass 'm' = 4 kg

Diameter of shaft 'd' = 10 mm = 1 × 10^{- 2} m

Shaft span 'l' = 50 cm = 0.5 m

 Eccentricity 'e' = 2 m = 2 × 10- 3 m

Shaft speed 'N' = 250 rpm

E = 2.0 × 10¹¹ Pa

 I = ( π/64) d ⁴  = (π /64)(1.0 × 10^{- 2} )4  = 4.9 × 10^-10  m4

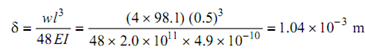
Critical speed wc  =

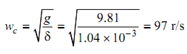
Angular speed of shaft w = 2π 250/60 = 26.18 r/s

Damping factor δ=  C/ Cc =C/2m w_c = 50 /(2 × 4 97)  = 0.064

                            = 1.457 × 10^-4 /0.928

                              = 1.57 × 10^{- 4} m

The dynamic load on the bearings

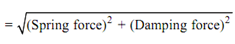
Spring force F_s  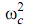= m X= (97)2  × 4 × 1.57 × 10^{- 4}  = 5.9 N

Damping force F_d = c ω X = (50 × 26.18) × 1.57 = 0.2 N

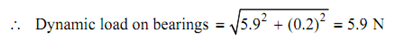
Deal load on the shaft = 4 × 9.81 = 39.24

∴ Maximum load on the shaft = 39.24 + 5.9 = 45.14 N

Maximum stress σ_max  =  (M/I)y= (FI/4)(d/2)(1/I)

 = (45.14 × 0.5/4) × (1 × 10^{- 2}/4)  ×(1/4.9 × 10^-10)

= 5.75 × 10- 9  N/m²

Power needed is based on the magnitude of torque that will be given by damping force.

T = c ω X × X = c ω X ²

 = 50 × 26.18 (1.57 × 10^{- 4} )²

= 3.23 × 10^{- 5}  Nm

∴             Power P = (2π NT)/60= 2π × 250 × 3.23 × 10^{- 5}/60

                                    = 8.45 × 10^{- 4} Watt.