Analysis of Single Degree Of Freedom System for Forced Vibration:

A single degree of freedom system is illustrated in Figure 1. It consists of mass m, damper of damping coefficient 'c' spring of stiffness k. It is subjected to an external harmonic force F_o sin wt. The vibration of mass occurs under the effect of the external force. That is why it is a case of forced vibration. The force body diagram of the body is also illustrated. Letting x and ? positive as illustrated in the Figure.

∴             m x + c x + k ( x + Δ) = mg + F_o  sin wt

             mx + cx + k x = F_o  sin wt                   ------------ (1)

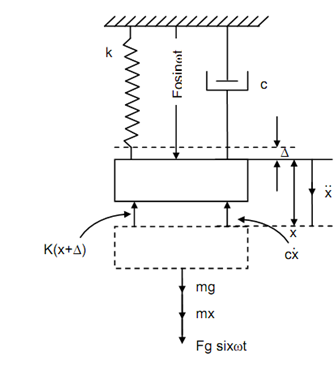
This may be noted down that the selection of static equilibrium position like reference line eliminates the have to consider the weight of mass in the force body diagram as initial extension in the spring takes case of weight of the body.

The universal solution of the differential Equation (1) will consist of two parts.

  x = Complementary fluctuation + Particular integral

The complemental function is attained by making right hand side zero. This is solution of the following differential equation

           mx'+ cx'+ k x = 0

This is the same equation represented by previous unit Equation (13). The solution of this equation is given by previous unit Eq. (22), that means

x = X ′ e^{-δ ωn t}  cos (ω d t + φ′)

In order to determine particular integral a trial function might be assumed as follows :

             x _p  = E sin ωt + F cos ωt           ----------- (16.2)

The essential condition is that this trial function must satisfy the differential Eq. (1). Putting value of x_p for x in Eq. (1), we obtain

m (- E w²  sin ωt - B w²  cos ωt ) + c ( E . w cos ωt - F w sin ωt )

+ k ( E sin ωt + F cos ωt ) = Fo  sin ωt

or            {E (k - mω² ) - cF w} sin ωt + {cE ω + F (k - mω² )} cos ωt = F_o  sin ωt

By Equating coefficient of sin wt and cos wt on both of the sides

 (k - mω² ) E - c ω F = F_o

cw F + (k - mω² ) F = 0

From these equations the values of E & F may be estimated.

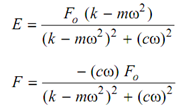
After putting the values of E and F in Eq. (2) the following is attained.

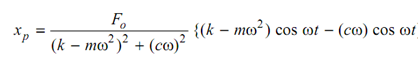
By rearranging the terms, the below expression is achieved.

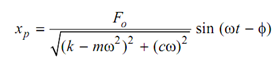
The phase angle φ is specified by

φ= tan -1 (cω /k - mω²)

or x _p  = F_o X sin (ωt - φ)         ----------------- (3)

Here

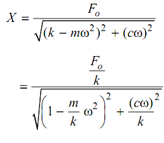
Let F_o /k = x_st  (The displacement when only Fo is acting as static force).

∴             X = DM × x_st                        --------------(4)