Example of Single Angle Struts:

Denote the strength of a sigle angle discontinuous strut, 60 × 40 × 6 if connected by (a) a single rivet, or (b) by two rivets in the line of the member.

Centre to centre between intersections is 1.4 m (f_y of steel is 250 MPa).

Solution

From the tables, Area of 60 × 40 × 6 angle = 5.65 cm², r_x = 1.88 cm, r_y = 1.11 cm, r_{u (max)} = 2.01 cm, r_{v (min)} = 0.85 cm.

Case 1 : Single Rivet Connection

l_eff = l = 1.4 m = 1400 mm

r_min = 0.85 cm = 8.5 mm

Slenderness ratio, λ = l_eff/r_rim = 1400/8.5 = 164.1 < 180∴ OK.

Elastic critical compression stress, f_cc =π² E/λ²

Where modulus of elasticity, E = 2 × 10⁵ MPa.

∴          f_cc= π² × 2 × 10⁵/(164.7)²= 72.8 MPa

∴          σ_ac = 0.6 f_cc.f_y/[(f_cc)n + (f_y)n]^1/n

where n = 1.4  Eq. (6.2).

∴  σ_ac   =          (0.6 × 72.8 × 250)/[(72.8)^1.4 + (250)^1.4]^1/1.4   = 72 × 250/(404.6 + 2275.7)^0.714

(0.6 × 72.8 × 250)/281 = 38.9 MPa

[This may also be obtained by reference to Table 2].

∴ Actual         σ_ac allowed is 80% of this value, i.e.

σ_ac allowed = 0.8 × 38.9 =31.1 MPa.

Strength of the member = Area × σ_ac (allowed)

= 565 × 31.1 = 17571 N ≈ 17.5 kN

This is shown in Figure(a).

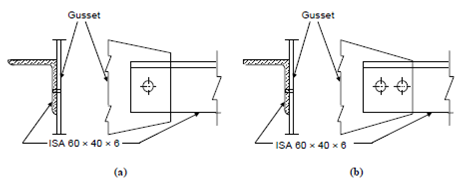
Figure

Case 2: Double Riveted Connection

Here the effective length = 0.85 × Actual length

= 0.85 × 1400 = 1190 mm.

∴          λ = 1190/8.5 = 140

By using Eq. (6.2) above or from Table 2, you will get the corresponding σ_ac as 51 MPa.

σ_ac allowed = 0.8 × 51 = 40.8 MPa

and strength of the member = 565 × 40.8 = 23052 N ≈ 23 kN This is shown in Figure.