Structural form and reduced form:

We  presented  the  simultaneous equation. These equations are  known  as  the  'structural equations' or 'behavioral equations'  as  they represent the  structure (of  an economic model)  or  the behavior  of  an economic agent (e.g.,  consumer or producer).  The  β and y' in are known as the structural parameters or coefficients. Recall that in the structural equations  both  endogenous and exogenous variables are  on  the right-hand side of each equation.

By  solving for the  M endogenous variables from the structural equations we can derive the reduced-form equations  and  the associated  reduced-form coefficients. A  reduced-form equation  is one where  each equation contains one endogenous variable and that endogenous variable is expressed solely in terms  of  the predetermined variables  and  the  stochastic disturbances.  To illustrate, let us consider the Keynesian model of income determination given at example.

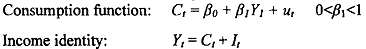
In this model C (consumption) and Y (income) are the endogenous variables and I (investment expenditure) is treated as an exogenous variable. While the first equation is stochastic in nature the second one is an identity.  As usual, the MPC (β₁) is assumed  to remain between 0 and 1.

We  obtain  after  simple  algebraic manupulation

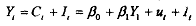
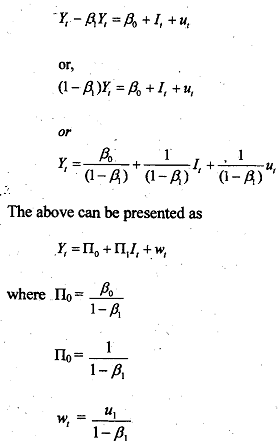
Equation  is  a  reduced-form equation.  It expresses the  endogenous variable  Y  solely as a function of the exogenous (or predetermined) variable and  the stochastic disturbance term.  no  and  n, are the associated reduced- form coefficients. Notice that these reduced-form coefficients are nonlinear chmbinations  of the structural coefficients(s).

Substituting the value of  fiom (13.26)  into C,  of (1  3.24), we obtain another , reduced-form equation:

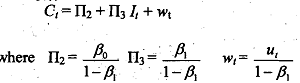
In  the context of econometric models, equations such as (13.25) or Q_dt  =  Q_st( (Quantity demanded equal to quantity supplied) are known as the equilibrium condition.  Identity states that aggregate income Y must be equal to aggregate expenditure  (i.e.,  consumption  expenditure plus  investment  expenditureb When  equilibrium  is  achieved,  the endogenous variables assume  their equilibrium values.