Simply Supported Beam with a Uniformly Distributed Load:

Let a simply supported beam AB of span l carrying a uniformly distributed load of w per unit length over the total length as illustrated in Figure .

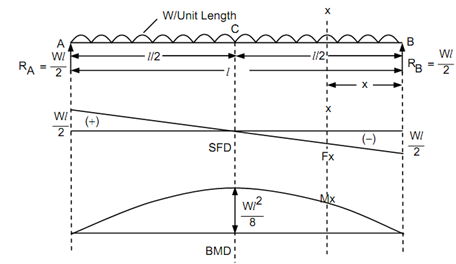
 Figure

Let us determine the reaction at the support B, taking moments around A and equating to zero,

R_B × l - w × l ×( l/2)          = 0

∴          R_B = + wl / 2

R_A = wl - R_B = wl -(  wl /2)= + wl/2

Let a section XX at a distance x from the end B.

The shear force equation,

Fx = - wl /2 + wx

SF at B,           F_B = - wl /2               (at x = 0)

SF at C,           F_C = - wl/2 + w(l/2)=0            (at x = l/2)

SF at A,           F_A = - wl/2 + wl = + wl/2         (at x = l)

The shear force at B is equal to -wl/2 and enhance uniformly by a straight line law to zero at C and continuous to enhance uniformly to +wl / 2 at A

The bending moment at section xx,

Mx =-wl/2 x-(w ´ x ´(x/2))

           =-wl/2 x - wx² /2

BM at A and B is zero

M_A = M_B = 0

M_C = wl/2(l/2) - (wl /2)wl/2)²

= wl²/4 -wl²/8 = +wl²/8

As the shear force is zero at midpoint of the beam, the maximum bending moment occurs at 'C'

∴          M_max = M_C = +  wl ² /8

The bending moment figure in the form of parabolic curve like the bending moment equation is parabolic equation.