Simply Supported Beam having an Eccentric Point Load:

Let a simply supported beam AB of length l subjected to eccentric point load W at C at a distance 'a' from the end A & B from the end B as illustrated in Figure .

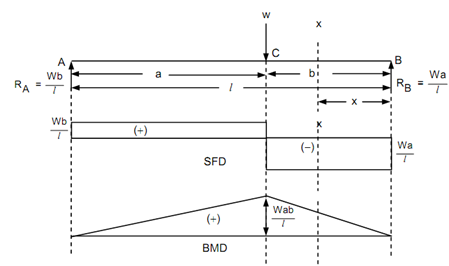
                                               Figure

To determine the reaction at the support B, taking moment around 'A'

R_B × l - W × a = 0

∴          RB = +( Wa /l)

            R_A = W - Wa/ l = + (W (l - a) )/ l = + Wb / l                      (where l - a = b)

Let a section XX among B & C at a distance x from the end B, that means. x < b. The shear force equation is as follows :

F_x = - Wa / l                              ('-'sign indicates right upward)

This equation is valid for the part BC. The shear force diagram is horizontal. Let a section XX among A and C at distance x from the end B, i.e. x > a.

The shear force equation is as follows :

 F_x = - Wa/ l + W = W (l - a)/l   = + Wb/ l

 (where l - a = b)

It is valid for the portion AC.

On the other hand, the shear force equation for the portion AC might also be obtained by considering the section among A and C at a distance 'x' from the end A.

The bending moment equation for the part BC is as follows :

M_x = + (Wa / l )× x ('+'sign indicates right clockwise)

The bending moment at A & B is zero. It enhances by a straight line law, and is maximum at C where the SF changes sign.

BM at C,         M_C  = + Wab / l                                  (at x = b)