Simply Supported Beam along a Triangular Load:

Simply Supported Beam along a Triangular Load Varying Gradually from Zero at both of the Ends to w per metre at the Centre

Let a simply supported beam AB of length l, subjected to a triangular load, varying slowly from zero at both of ends to w per unit length at centre as illustrated in Figure

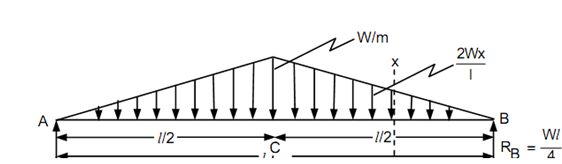
Figure

As the load is symmetrical, thus, the reactions RA and RB shall be equal.

 R_A  = R_B  = (1/2)´(1/2) × w × l = wl/4

Taking moments around A,

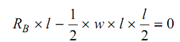
R _B × l - (½) × w × l × (l/2) = 0

∴          R _B   =+ wl/4

            R_A   =( ½) × w × l - R_B = wl /2- wl /4= + wl/4

Let a section XX at a distance 'x' from the end B.

The shear force at XX,

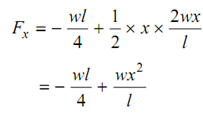
F  =-( wl/4)  + (1 /2)× x × (2wx/ l)

=- wl /4 + wx²/l

SF at B,

F_B   =- wl/4                              (at x = 0)

SF at C,

F B   =- (wl/4) + (w/l).(1/2)² ( at x =  l/2)

=- (wl/4) + (wl/4) = 0

The shear force illustration is in the form of parabolic curve as the shear force equation is parabolic equation.

The bending moment at XX,

M _x  = (wl/4)x - (1/2) x × (2wx/l) × (x/3)

        = (wl/4)x - (wx³)/3l

The BM at A & B is zero. The bending moment shall be maximum, where the SF changes sign. In this case, the maximum bending moment takes place at x = 1/2 , i.e. at C.

M _max  = M _C  = (wl/4)(l/2) -(w/3l)=(l/3)³

            = wl² /8 - wl²/24 = 2wl²/24 = + wl²/12

As, the bending moment equation is cubic equation, the bending moment diagram is in the form of cubic curve.