Simply Supported Beam along a Gradually Varying Load:

Simply Supported Beam along a Gradually Varying Load, from Zero at One End to w per metre at the other End

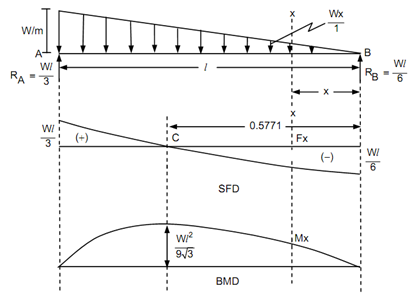
Let a simply supported beam AB of span l carries a slowly varying load from zero at one end to w per unit length at the other end as illustrated in Figure .

Taking moments around A and equating to zero,

R_B   × l - (½) × w × l × (l/3) = 0

∴  R _B  = + wl/6

R_A   = (½) × w × l - R_B = (½ )wl - wl/6 = + wl/3

Figure

The shear force at any particular section XX at a distance x from the end B.

F_x  =-  wl /6 + (½)×(w/l) × x × x = - (wl/6) + (wx² /2l)

 SF at B,

F_B   =- wl/6                       (at x = 0)

SF at A,

F_A   =- (wl/6) + (wl /2)=+ (wl/3)             (at x = l)

The bending moment at any particular section XX at a distance x from the end B.

M_x   = wl/6 x - (1 /2)× (w /l)× x × x × (x/3)

M _x  =  wlx/ 6   -  wx³/ 6l

The BM at A and B is zero (whereas x = l & x = 0).

To determine the maximum bending moment, compare the shear force Eq. (i) to zero.

- wl/6  + wx²/2l           = 0      

      wx²/ l = wl /3

x²  = l² /3

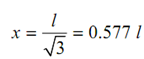
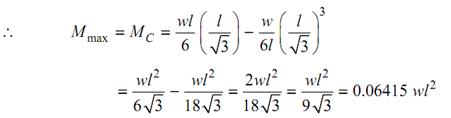
The shear force diagram is in form of parabolic curve as specified by in Equation (i). As, the power of 'x' in the moment equation is of order 3, the bending moment diagram is in the form of cubic curve.