Important features of the dummy variables:

Before proceeding further it  is essential to discuss some of the important features of the dummy variables which are as follows:

1) In the above models  we  have introduced  only one  dummy  variable, D,  to distinguish between  two  categories, male  and female with D₁ = 1  denoting maje and D_i = 0 denoting female. Now what happens if instead of one dummy variable two  dummy variables D₁, and  D₂,  are  introduced  in  the model,  one each for male and female? Model can now be written as  .

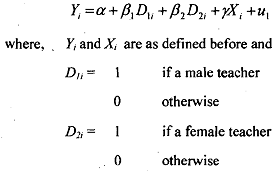
Due to perfect collinearity between D₁and D₂  (i.e.,  perfect linear relationship) model cannot  be  estimated. This  can  be  more clearly explained with  the  help of  the following data table.

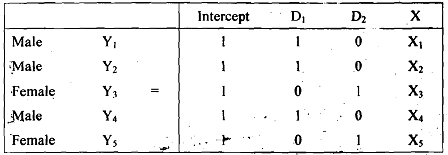
From the above table it  is easy to verify that D₁ and D₂  are perfectly collinear as D₁ =  (1  -  D₂)  or D₂ = (1-  D₁).

There are,  however,  a  number  of  ways  of resolving  this  problem but the simplest one is by  assigning the dummies as we had done  in model and using  orlly  one .dummy variable  if  there are  two  categories of  a  qualitative variable.

Rule of Thumb:  If a qualitative variable has m categories, introduce only (m -1) dummy variables Thus  if  a qualitative variable has 4  characteristics, introduce only  3 dummy variables. If this rule  is not  followed, we  shall fall into what  is known  as the dummy variable trap, i.e., a situation of perfect multicollinearity.

2) The assignment of values 0 and 1 to two categories like rural and  urban, or educated and uneducated  etc.,  is  arbitrary.  For  example  in  our model  10.5 instead of assigping 1 to male teacher and 0 to female teacher we could have assigned value 1  to female teacher and 0 to male teacher (and the coefficients would  change accordingly).  In  such  a  case  what  is  of importance is  the interpretation of results. Thus in  interpreting the results of the models that use dummy  variables  it  is critical to know  how  the  values  1 and  0 are assigned.

The category that is assigned a value 0 is often referred to as the base category or benchmark category and all the comparisons are made with reference to this category. In model female school  teacher which  is assigned value 0 is the base or benahmark category.

3)  The coefficient attached to the dummy variable (for example, β in model) is  referred to as the differential intercept coefficient because  it  tells by  how much  the  value  of  the  intercept  term  of  the  category that receives value  1 differs  from that of the base category.