Theory of Simple Bending:

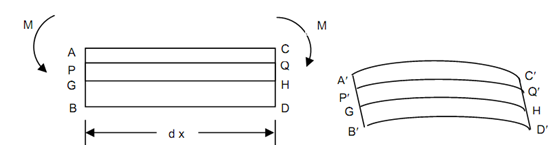
Let a cantilever subjected to a clockwise moment M at the free end. The cantilever is subjected to a constant bending moment M at all of sections of the beam. Assume AB & CD is two sections at a distance dx apart, as illustrated in Figure .

Since the cantilever is subjected to a constant bending moment M, the beam bends into a circular arc. The top of fibres of the beam are subjected to tension.

The topmost layer AC has elongated to A′C′. The lower layers, below the topmost layer of the beam have also elongated, however to a lesser degree. Now, we come to the layer GH. This layer has not suffered any modification in its length. This layer is said the neutral layer or neutral plane.

    (1) Before Bending                               (2) After Bending

  Figure

All of the layers below GH have compressed to variable amounts. Thus, all the bottom fibres of the beam are subjected to compression. The bottommost layer BD has compressed to B′D′.

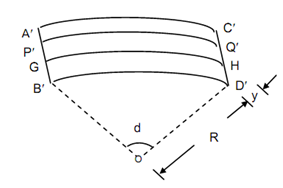
Let the projections of A′B′ and C′D′ meet at O, as shown in given Figure.

Figure

Let dθ be the angle between the planes A′B′ and C′D′ and R be the radius of the neutral layer. Consider a fibre P′Q′ at a distance y from the neutral layer.

Original length of this fibre = PQ

                                              = dx

                                             = R dθ

after deformation, this fibre occupies the position P′Q′.

Now, the length of the fibre   P′Q′= (R + y) dθ.

Increase in length of fibre       PQ = P′Q′ - PQ

                                                     = (R + y) dθ - R dθ = y dθ

Strain in fibre PQ,       ε = Increase in length/ Original length

                              ∴      ε = ydθ / Rdθ = y/R

Let σ be the stress in fibre PQ.

Then,   ε = σ/ E , where E is the Modulus of Elasticity of the material.

∴          ε = σ / E = y/ R

∴          σ = (E / R)× y

Therefore, the stress intensity in any fibre is proportional to the distance of the fibre from the neutral layer.