Position of Neutral Axis:

Let us look at Figure, which illustrated the cross section of a beam.F

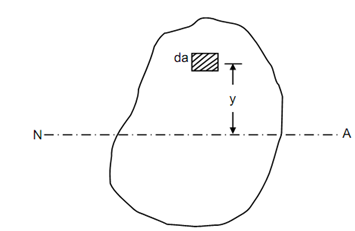
Figure

Consider an elementary area da at a distance y from the neutral axis. Let the bending stress on the element be σ.

The force on the elementary area = σ × da    

Force over the entire cross-section = Σ (σ × da)

From equilibrium considerations, the entirety compressive forces and tensile forces on the section should add to zero.

Thus, mathematically,

∴          Σ (σ × da) 0

We have already seen that σ = (E/ R) × y. Thus, on substituting the value of σ, we achieved,

Σ (E / R) × y × da = 0

i.e.    (E/ R) ∑ y da = 0

As E/R is a constant for a particular section, we have Σ y da = 0. It means that the moment of the whole area about the neutral axis is zero.

Here, y × da is the moment of area da about the neutral axis and Σ (y × da) is the moment of entire area of cross section about the neutral axis. Thus, the neutral axis of the section is situated in such a way that the moment of entire area about it is zero. We know that the moment of an area about the centroidal axis is zero. Hence, the neutral axis of a section always passes through its centroid.

Thus, to locate the neutral axis of a section, find the centroid of the section. After that, draw a line passing through this centroid and normal to the plane of bending. This line is the neutral axis of the beam section.