Signaling Requirement 1: After observing any message mj from M, the receiver must have a belief about which types could have sent mJ. Denote this belief by the probability distribution μ(ti,1 mj), where u(ti | mj) ≥ 0 for each ti in 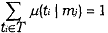
Given the sender's message and the receiver's belief, it is straightforward to characterise the receiver's optimal action. Applying requirement 2 to the receiver therefore yields:
Signaling Requirement 2R: For each mj in M, the receiver's action a*(mj) must maximise the receiver's expected utility, given the belief μ(ti,1 mj) about which types could have sent mj. That is, a*(mj) solves 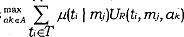
Requirement 2 also applies to the sender, but the sender has complete information (and hence a trivial belief) and also moves only at the beginning of the game, so requirement 2 is simply that the sender's strategy be optimal given the receiver's strategy:
Signaling Requirement 2s: For each ti in T, the sender's message m*(ti) must maximise the sender's utility, given the receiver's strategy a (mj). that is,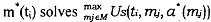
Finally, given the sender's strategy m*(t,), let Tj denote the set of types that send the message m,. That is, t, is a member of the set TJ if m*(ti) = mj. If Tj is nonempty then the information set corresponding to the message m, is on the equilibrium path; otherwise, m, is not sent by any type and so the corresponding information set is off the equilibrium path. For messages on the equilibrium path, applying requirement 3 to the receiver's beliefs yields:
Signaling Requirement 3: For each m, in M, if there exist t, in T such that m (t,) = m,, then the receiver's belief at the information set corresponding to m, must follow from Bayes' rule and the sender's strategy:
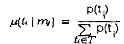
Definition: A pure strategy perfect Bayesian Nash equilibrium in a signaling game is a pair of strategies m*(ti) and a*(mj) and a belief μ(ti,1 mj)satisfying signaling requirement 1, 2S, 2R and 3. If the sender's strategy is pooling or separating we call the equilibrium is pooling or separating respectively.