Example of Signaling Game:
Each type is equally likely to be drawn by nature; we use (p, 1 -p) and (q, 1 -q) to denote the receiver's beliefs at her two information sets. The four possible pure strategy perfect Bayesian equilibria in these two types, two message game are: (1) pooling on L; (2) pooling on R; (3) separation with t, playing L and t2 playing R; and (4) separation with tl playing R and t2 playing L. We analyze these possibilities in turn.
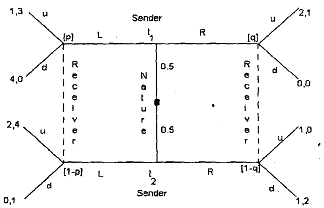
1) Pooling on L: Suppose there is an equilibrium in which the sender's strategy is (L, L), where (m', m") means that type tl chooses m' and type t2 chooses m". Then the receiver's information set corresponding to L is on the equilibrium path, so the receiver's belief (p, I -p) at this information set is determined by Bayes' rule and the sender's strategy: p = 0.5, the
prior distribution. Given this belief (or any other belief, in fact), the receiver's best response following L is to play u, so the sender's type t1 and tearn payoffs of 1 and 2 respectively. To determine whether both sender's types are willing to choose L, we need to specify how the receiver would react to R. If the receiver response to R is u, then tl's payoff from playing R is 2, which exceeds tl's payoff of 1 from playing L.
But if the receiver response to R is d then t, and t earn payoffs of 0 and I (respectively) from playing R, whereas they earn 1 and 2 (respectively) from playing L. Thus if there is an equilibrium in which the sender's strategy is (L, L) then the receiver's response to R must be d, so the receiver's strategy must be (u, d), where (a', a") means that the receiver's plays a' following L and a" following R. It remains to consider the receiver's belief at the information set corresponding to R, and optimality of playing d given this belief. Since playing d is optimal for the receiver for any q ≤2/3, we have that the [(L, L), (u, d), p = 0.5, q] is a pooling perfect Bayesian equilibrium for any q ≤ 2/3.
2) Pooling on R: Next suppose the sender's strategy is (R, R). Then q = 0.5, so the receiver's best response to R is d, yielding payoffs of 0 for tl and 1 for t2 but t, can earn 1 by playing L, since the receiver's best response to L is u for any value of p, so there is no equilibrium in which the sender plays (R, R).
3) Separation with tl playing L: If the sender plays the separating strategy (L, R) then both of the receiver information sets are on the equilibrium path, so both beliefs are determined by Bayes' rule and the sender's strategy: p = 1 and q = 0. The receiver's best responses to these beliefs are u and d, respectively, so both sender types earn payoffs of 1. It remains to check whether the sender's strategy is optimal given the receiver's strategy (u, d). It is not: if type t2 deviates by plying L rather than R then the receiver responds with u, earning t a payoff of 2, which exceeds t2's payoff of I from playing R.
4) Separation with t1 playing R: If the sender plays the separating strategy (R, L) then receiver's belief must be p = 0 and q = 1, so the receiver's best response is (u, u) and both types earn payoffs of 2. If t1 were to deviate by playing L, then the receiver would react with u; tl's payoff would then be 1, so there is no incentive for tl to deviate from playing R. Likewise, if t2 were to deviate by playing R, then the receiver would react with u; t2's payoff would be then 1, so there is no incentive for t2 to deviate from playing L. Thus, [(R, L), (u, u), p = 0, q = 11 is a separating perfect Bayesian equilibrium.