Conical Shells:

Stresses

In the shape of conical containers Shells shall normally be supported around their upper rim. Let a conical shell of total height h and supported at the top as illustrated in Figure.

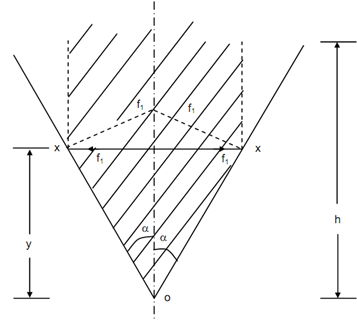
Figure

Let any level XX at a height y from the apex O.

At this level,            r₂  =∞

By using the expression for stresses in a doubly curved shell,

f₁ /r₁ +  f₂ /∞ =  p/t

f₁=  pr₁ /t

 where r₁ is radius of the circumferential curvature. From the geometry curvature of the shell, we get

p = w (h - y)

r₁= y ( tan α / cos α)

∴          f₁ = (w (h - y) )/ t × ( y tan α /cos α)

It is the hoop stress at the level XX. For this stress to be maximum,

df₁ / dy = (w tan α / t cos α )(h - 2 y) = 0

∴ y=h/2

Substituting y = h /2 , we get

Maximum hoop stress  = w(h-(h/2))(h/2)tan α / t cos α

= w h2  tan α / (4t cos α)

Stress in the meridional direction f₂ may be calculated by letting the total weight of water contained in the shaded portion of the vessel as illustrated in Figure .

This weight is resisted by the vertical component of the induced material tension on the circumference XX.

 Therefore,

f₂ 2π y tan α t cos α= w (h - y) π y² tan ² α+ w π y² tan² α (y/3)

∴          f₂  = (w tan α/2t cos α) (hy - (2/3)y²)

For this stress to be maximum,

df₂  /dy= (w tan α/2t cos α) (h - (4y/3))

∴          y = 3h

Maximum meridional stress,

= ( w tan α/2t cos α) ( 3h² /4 - 3h²/8)

= (3/16) (wh2  tan α/ t cos α  )