Calculating Shearing Stress:

As per perpendicular axis theorem,

I_zz = I_xx + I_yy

From a circular section,

I xx  = I yy =  (π /64 )d ⁴

where d is refer to the diameter of the circular shaft.

Hence, J = I zz =  πd ⁴ / 32

The term J / (d /2) is known as torsional section modulus or polar modulus, mention by Zp. It is same to section modulus, Z, which is equal to M/l.

Therefore, polar modulus for a solid shaft

Z p  = πd ⁴/32 .2 /d = πd ³ /16

A hollow circular section is just like a circular section with only difference in the value of J. J for a hollow section can be calculated as different of J values of sections of outer diameter (d0) and inner diameter (d_i).

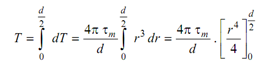
where respectively d₀ & d_i are the outer and inner diameters.

Eq. may be compared with equation of bending  M/I = σ/ y = E / R.

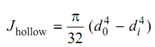
The expression τ_r /r corresponds to σ/y , T /y corresponds to M/I  and Gθ /l corresponds to  E . The expression GJ corresponds to expression EI.

The term GJ is called as torsional rigidity and the term EI is called flexural rigidity.

It can be noted that:

(a)  T / θ, i.e. torque needed for unit twist, is called as the torsional stiffness of the shaft.

 (b) T / (θ/ l), that means torque divided by the angle of twist per unit length, is called the torsional rigidity.

Units of various quantities mentioned above are usual. T is normally measured in Nm, τ_r, τ_m and G have units of N/m² (Pa) or N/mm², l is measured in m. θ contains radians as units.