Shear Stress Distribution into Triangular Section:

Let us assume a triangle of base b and h. Its centroid is at a distance h/3 from the base.

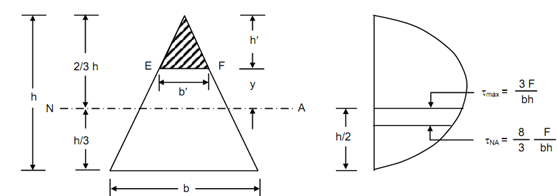
                      Beam Cross-section                         Shear Stress Distribution

Figure

Assume the shear stress at the plane EF, at a distance y from the neutral axis be q.

Assume b′ & h′ be the width & height of the triangle above the plane EF.

From same triangles,

b / b′=  h/ h′

b′ = bh′ / h

h′ =  ((2/3) h - y )

b′ =  (b/ h) ( (2/3) h -  y )

Centroid of the triangle above the plane EF, through the neutral axis = ( y +( h′ /3 ))

On putting the value of h′ = y + (1/3)((2/3)h -  y ) =(2/3)(y+(h/3))

Moment of this triangular area around the neutral axis,

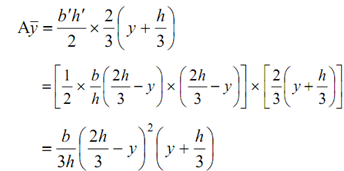
∴ Shear Stress, 

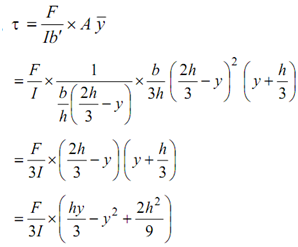
For shear stress τ to be maximum, dt / dy = 0 ,

                      ((h /3) - 2 y  = 0

∴          y = h/6

The height through the base of the triangle is

                                          h/ 3+ h/6    = h/2

∴ Maximum shear stress is at particular distance h/2 through the base of the triangle, that is also at a distance of h/6 from the centroidal axis.

Putting y = h/ 6 in the equation for the shear stress, we achieved,

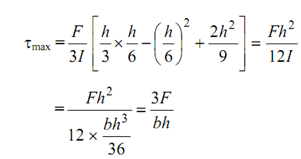
The shear stress at the neutral axis, that means y = 0, is as follows :

τ_NA = (F /3I ) (2h²/9)=     2Fh ²/27I

=2Fh²/(27 × (bh³/36) = (8/3) ×(F/bh)

The shear stress distribution diagram might be seen in Figure.