Shear stress distribution in the Web:

Width of section at particular distance y from the neutral axis = b.

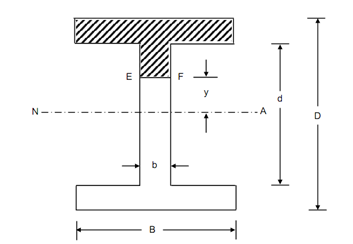
Beam Cross-section

Figure

Area above the plane EF = area of flange + area of web upto EF = B (  D - d) + b ((d/2) - y )

Centroidal distance of the flange area through the neutral axis, = (1/2) ((d/2) + y)     

Centroidal distance of the web area through the neutral axis, =(1/2)  ((d/2)+y)

Moment of both the areas around the neutral axis,

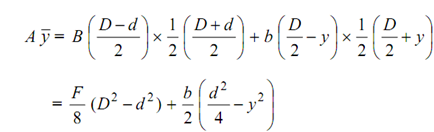
∴ Shear stress, τ = (F/ Ib) × A

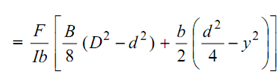
∴  The shear stress contain also a parabolic distribution in the web.

At the junction of the flange & web, i.e. at y = d/2   ,

∴ Shear stress, τ   = (F/ Ib)  ×   (B/8) (D ² - d ² )

Now, it might be noticed that at the junction of the flange & web, the shear stress suddenly changes from ( F /8I )(D2 - d 2 ) to (F / Ib )× (B/8) (D² - d ² ) .

At the neutral axis, that means at y = 0, the shear stress is maximum and this is as follows

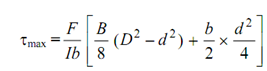
The shear stress distribution might be seen in Figure.

From the shear stress distribution diagram, we wind up that most shear stress is taken up by the web. This is extremely important in the design of beams by using I and T sections.