Shear Stress Distribution in the Circular Section:

Now we will consider a circular section of radius R.

Consider dy be the thickness of an elementary strip at a distance y from the neutral axis.

Moment of this trip around the neutral axis = (b dy) y

Moment of area above the plane EF about the neutral axis,

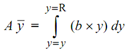
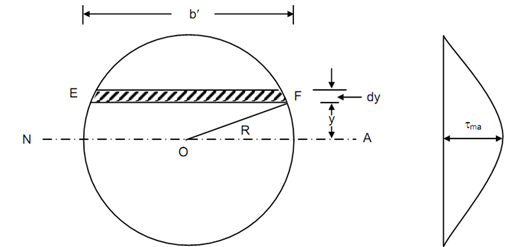
                           Beam Cross-section                           Shear Stress Distribution

 Figure

But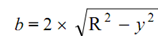 

or         b² = 4 (R² - y²) On differentiating, we achieved,

2b db = 4 (- 2y) dy

= - 8y dy

∴  y dy = -(b db/4)

When y = y, b = b and y = R, b = 0.

Now modifying the integration variable from y to b,

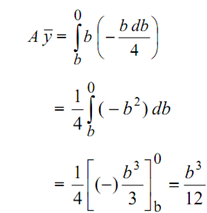
∴The shear stress,       

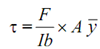
=  (F /lb) ×(b³/12) = Fb² /12I

=  (F/ 12I ) × 4(R ² - y ² )

= ( F / 3 I) (R ² - y ² )

Therefore, shear stress contains a parabolic variation. The shear stress is maximum while

y = 0, at the neutral axis.        

∴          τ_max = (F / 3 I) × R ²

=          (FR² /3)× (4/ πR ⁴)  (since, I = πR⁴ /4)

=(4/3)  × (F/ πR ²)

=  (4/3) × (F / Cross - sectional area)

The shear stress is zero at top and bottom layers, i.e. at y = R,

∴          τ_min = (F/3I) (R ² - R ² ) = 0

Average shear stress = Shear force/ Area of cross section of beam    =F/ πR²

∴          τ_max =(4/3)( F/ πR²)

=(4/3) τ_average