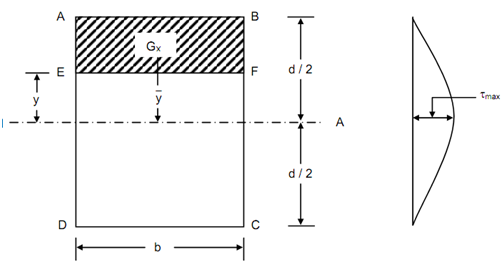
Shear Stress Distribution in Rectangular Section:

Let us assume a rectangular section of width b & depth d subjected to shear force F.

Let τ be the shear stress at any level EF, as denoted in Figure

Area ABFE, A = b (( d/  2) -  y

Distance, = y +( ½) (( d/2)-y)

=( ½)   ((d/2)+  y )

     Shear Stress Distribution                     Beam Cross-section

  Figure

Moment of area ABFE around the neutral axis,

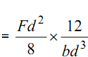
    = b (( d/2) -  y ) × (1/2) (( d/2) +  y

=          (b /2)( (d ²/4) - y 2 )

∴ Shear stress, τ = (F / Ib )×  

= (F / Ib )× (b /2) (( d² /4) - y ² )

= ( F/2I) (( d² /4) - y ² )

∴  Shear stress contain a parabolic variation.

The maximum shear stress occurs while y = 0, at the neutral axis.

∴          τ_max =(F/2I)( (d ²/4)-0) = Fd ²/8I

=          (Fd ²/8) × (12/bd ³)

=  (3/2) × ( F/ bd)

= =  3 ×(F/ Cross - sectional area)

The shear stress is zero at the top and bottom layers, i.e. at y = ± (d/2).

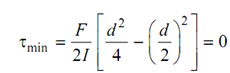
Average shear stress = Shear force / Area of cross section of beam

τ_average = F / bd

∴          τ_max = (3/2) × (F/ bd)

              τ_max = 1.5 × τ_average