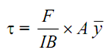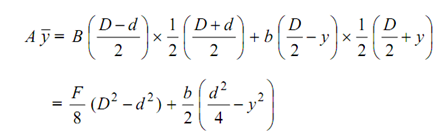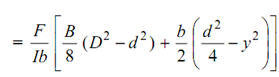Shear Stress Distribution in I & T Sections:

I-Section:

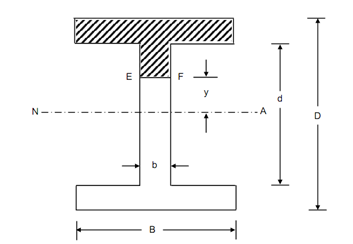
Let us take an I-section along flange width B and whole depth D. Let b & d be the thickness of web & depth, respectively.

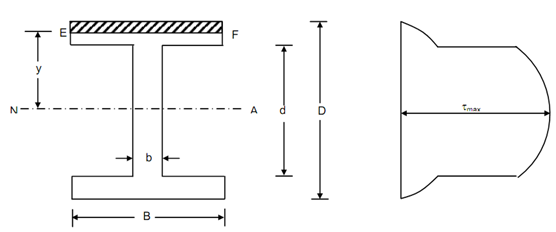
                         Beam Cross-section                              Shear Stress Distribution

Figure

Shear Stress Distribution in the Flange

Width of section at distance y from the neutral axis = B

Area above the plane EF = B (  (D / 2) - y )

Centroidal distance of this area through the neutral axis

=  (½) (( D/2)-y) + y = (1/2)((D/2)+y)

Moment of the area above the plane EF around the neutral axis,

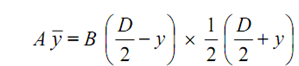
          = (B /2)( D ² /4) -y²)

∴ Shear stress,

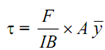
        = (F/ IB)   ×  (B /2) (D²/4 - y²)

        = (F/2I) ( D²/4 - y²)

Therefore, the shear stress contains a parabolic distribution in the flange.

At the top of I-section, that means at y = D/2, the shear stress, τ = 0.

At the junction of the flange and web, i.e. at y =d/2 ,

Shear stress, τ = (F/2I )((D²/4 )- (d²/4)) = (F/8I) (D ² - d ² )