Calculation of Shear Stress Distribution in Beams:

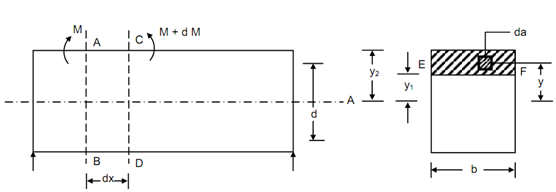
Let us assume two cross sections AB & CD at a distance dx apart, in a beam under transverse loading.

Let M & M + dM be the bending moments at the sections AB & CD, respectively, as illustrated in Figure .

Assume da be an elementary area at a distance y from the neutral axis.

Assume σ₁ and σ₂ be the bending stresses at sections AB & CD respectively, on the elementary area.

∴ σ₁ = (M / I )× y and σ₂ = ( (M + dM ) / I) × y

                       Loaded Beam                                              Beam Cross Section

 Figure

At the section the force on the elementary area AB = σ₁ × da = (M_y/ I )× da

 At the section, the force on the elementary area CD = σ₂ × da =(((M + dM ) y )/I )× da

The unbalanced force on the elementary area = (dM/ I ) × y × da

Letting any level EF, entirety unbalanced force above the level EF among the two sections AB & CD, is as:

          ∑ (dM / I )× y × da

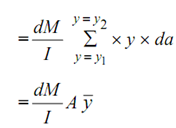
Here, Ay is the moment of area above level EF around the neutral axis. To make sure that the part of beam above the level EF and among the sections AB & CD is in equilibrium, like equilibriant to the unbalanced force, the beam section at the level EF should offer a shear resistance.