Bending Moment: General:

For any rigid or deformable body, the rotational equilibrium might be ensured if the algebraic total of moments of all of the forces working on the body in the x, y, z directions are separately zero .

Mathematically,

∑M_x = 0, ∑M_y = 0, and ∑M_z = 0.

Here M_x, M_y, M_z are the moments of forces taken around x, y, z axes.

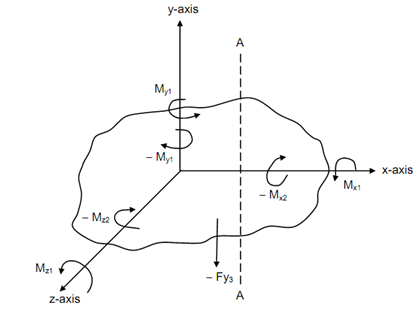
Figure: Equilibrium of a Body under a System of Moments

These moments are general moments & their +ve or -ve sign shall based on, whether the moments are clockwise or counter-clockwise.

∑M_x = Algebraic total of moments of all the forces around x axis =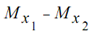

∑M_y = Algebraic sum of moments of all the forces around y axis =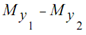

∑M_z = Algebraic sum of moments of all of the forces around z axis =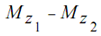

Now, consider a section A-A parallel to y-z plane in the body .The right hand portion is eliminated and the moments exposed on section in the left hand portion of the body are illustrated in Figure .The three moments, M_x, M_y, M_z are illustrated to be positive for the sake of convenience. A little thought shall show that all of the moments do not produce same type of stresses on the section. "M_x, working on section x" create a twisting action on the section. M_x renamed as M_xx is a torque and generates torsional shear stresses on the section. The remaining moments M_y and M_z working on section x, renamed as M_xy, and M_xz generate a bending of the body around y or z axis and produce linearly varying tensile and compressive stresses on the section. These moments are called as bending moments on a section A-A. Therefore, we see that same moments might be twisting or bending moments, based on the orientation of the section considered. y-axis.