Simply Supported Beams:
In particular case of simply supported beam, the point of contraflexure is extremely important. Where the BM changes sign at some of point, the bending moment shall be zero and that point is called as the point of contraflexure.
Simply Supported Beam along a Point Load at its Mid-span
Let us assume a simply supported beam AB, span l, carries a point load W at its mid-point 'C' as illustrated in Figure .
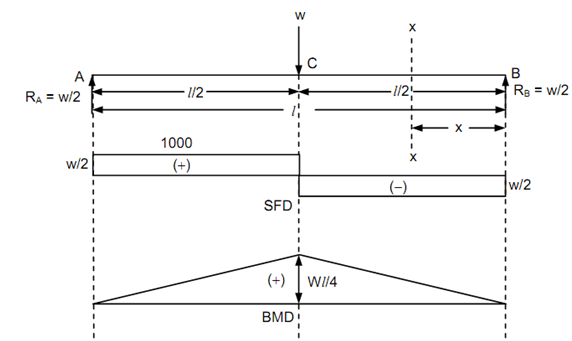
Figure
Let us first determine the reaction at the support B by taking moments around A, and equating to zero.
RB × l - W ×( l/2) = 0
∴ RB = + W/2
RA = W - RB = W - (W/2) = + W/2
(Conversely since the load is at the mid-point of the beam, the reactions at the supports RA = RB = W/2.)
Let a section XX among B & C at a distance 'x' from the end 'B'. The shear force equation is
Fx = - W/ 2 ('-' sign indicates right upward)
This equation is valid for all of the values of x from 0 to l/2 . As there is no loading among B & C, the shear force diagram is horizontal, that means SF remains unchanged. Let a section XX among A and C at a distance 'x' from the end 'B'.
The shear force equation is
Fx = - W /2 + W = + W /2
This equation is valid for all values of x from l/2 horizontal to l. The shear force diagram is horizontal.
On the other hand, the shear force equation might also be written by considering a section between A & C at a distance 'x' from the end A.
The bending moment at A & B is zero. It enhances by a straight line law, and is maximum at the centre of the beam where shear force changes sign.
The bending moment equation is
Mx = + (W/2 ). x ('+' sign denoted right clockwise)
BM at C, MC = Wl /4 (whereas x =l/2)