Endogenising Unemployment:

We  need  to  find an expression for V,.  For  that you may proceed  the similar way as in case of  (1')  and  (1")  .  From the worker's problem, consider V,,  such that 

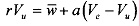
where  a  is a job acquisition rate i.e., the rate at which the capital gain V_eⁿ  -V_u is realised, and  i7 w the current return from being unemployed,  i.e., unemployment benefit. See that V,  must be equal to  V_eⁿ in equilibrium. For,  it can never be efficient for firms  to hire workers who  shirk. If  they shirk ever, they shirk always, so they are unproductive. We can now solve equations (5.2) and (5.4) together we get,  

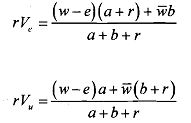
In the above equation we do not have q as no one is shirking in equilibrium. By plugging back  rV_u into the NSC (5.3) above, we get  

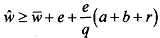
On the basis of this inequality, we get two additional implications viz., 

i)  higher the unemployment benefit, higher is the critical wage. 

ii)  higher  the flow out of unemployment  (a)  ,  higher is the critical wage. 

We are now in a position to solve the parameters of the model. In  the  long-run equilibrium, we have the following steady state relationship between  total  labour  fore N,  employment L and  unemployment U = N  - L. Thus, it must be the case that flows out of unemployment equal flows in. Hence,  

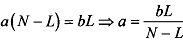
Since N  - L = U (unemployment), we have  aU = a  (N -L).  This gives the number of workers who find jobs  at any given time. On  the other hand,  bL gives the number of workers who lose their jobs  at any given time  (with no shirking). Substituting  back into (5.9, we get  

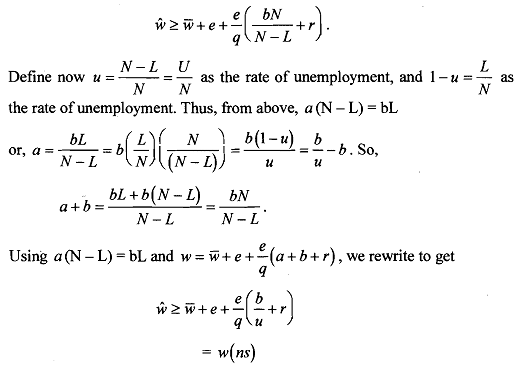
Equation  (5.6)  shows  that the  non-shirking  wage  requires some unemployment  at equilibrium.  Thus, (5.6) becomes a quasi-labor  supply function. As the employment rate approaches 0, the critical wage tends  toward infinity.  In  equilibrium

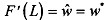i.e.,  labor demand  intersects quasi- labor supply.