Parallel Resonance:

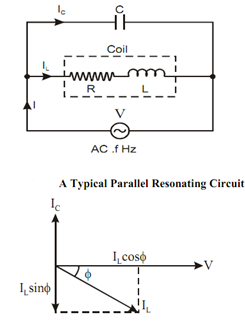
Given figure represents a parallel resonating circuit where a coil is connected in parallel with a capacitor C and the combination is connected across an AC voltage source of variable frequency. Figure represents the vector diagram of the given circuit.

                Vector Diagram of the Parallel AC Circuit

Let       I_C  = The current through the capacitor,

              I_L = The current through the coil,

I = Vector sum of I_L and I_C, that is the source current,

V = Supply voltage, V_R = Drop across R, V_L = Drop across L, V_C = Drop across C,

φ = p.f. angle of the coil (i.e. the angle of lag of IL with respect to V),

Z_L = Coil impedance, and

X_C = Capacitor impedance (or simple capacitor reactance).

Here  I_C  = V/ X_C

And

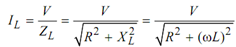
cos φ= R/ Z

At resonance the capacitive current should be equal to the inductive part of the coil current, that means the imaginary components of I_L and I_C should cancel each other at resonance.

i.e.              I_C  = I _L  sin φ

 or        V / X _C    = ( V / Z _L) × (X _L/ Z _L)

where  sin φ= X _L / Z _L ,

or         (Z _L )² = X_C X_L

Also

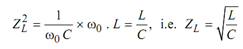
 [ω₀ represents resonance frequency]

or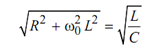       

               (ω_o )²L² = (L/C)-R²

i.e.          (ω_o )²L² = (1/ LC)-R² /L²

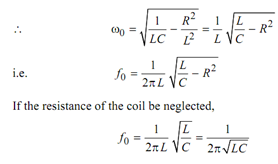
Again, at resonance, as the reactive components of I_L and L_C balance each other, the only remaining part of the current is I_L cos φ (= I)

                                                      I = I _L  cos φ

or,

                                          V / Z_Ω  =  V/ Z _L .  (R          / Z _L)     [Z_Ω = equivalent impedance of parallel circuit.]

or,

Z _Ω =( Z _L)²  /R =  (L/C )/R =   L/(CR)    [?         Z_L =       √(L/C)]

Then, the equivalent impedance of the parallel resonating circuit is L/CR at resonance. This impedance is called as dynamic resistance of the parallel circuit. In general R being loss, this impedance is extremely high at resonance and then the current is much lower in the parallel circuit. Then, this circuit is also called as rejector circuit.