Calculated unbalanced forces:

In an opposed piston engine the strokes of bottom and top pistons are 760 mm and 1040 mm respectively and the reciprocating parts weigh 54210 N and 39650 N respectively. The connecting rod lengths are respectively 2080 mm and 3040 mm. The engine speed is 123 rpm. Calculated unbalanced forces.

Solution

The sketch of the engine is illustrated in Figure 5.

This kind of engine, normally an internal combustion kind, contains a single cylinder in which two pistons move along the line of stroke. The pistons move towards or away from each other. The piston closer crank shaft operates the central crank and other piston that is away from crank shaft operates two cranks on the two of side of the central crank. Therefore the two pistons move outwards or inwards together as the side cranks are set at 180^o along the central crank. The piston that is away from crank shaft transmits motion to the cranks from two sides rods linked to a crosshead. The rods are linked to the connecting rods of appropriate length. Therefore the reciprocating parts of this piston weigh more than those of the first piston.                              

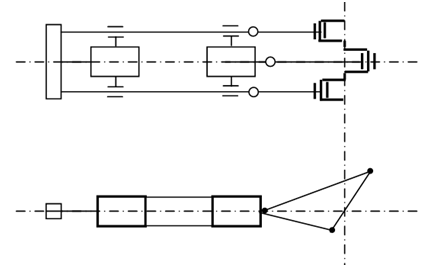
This kind of engine has been designed as a slow marine engine and as in aircraft engine.

This engine offers the advantage of couple balancing and primary force. It will be attained by making products of reciprocating mass and crank radius equivalent for central crank and side cranks. As the reciprocating mass is less for central crank its radius should be larger.

Bottom piston is closer to crank shaft, r _b  = 1040 /2= 520 mm

Top piston is further away from crank shaft, r_o  = 760/2 = 380 mm

Therefore,

Reciprocating weight along top piston, R_o  = 54210 N

Reciprocating weight along bottom piston, R_b  = 39650 N

R_b r_b  = 39650 × 520 = 20.6 × 106  N R_o r_o  = 54210 × 380 = 20.6 × 106  N R_b r_b  = R_o r_o  = W (say)

Therefore, primary forces are balanced ------------------- (i)

The three forces act on the crank shaft as illustrated in Figure.

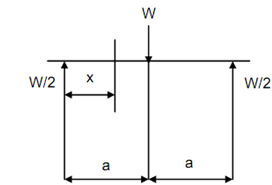
Select any point at a distance x from left crank. Take moment around this point.

M = (W /2) x + (W/2) (a - x) - (W/2) (2a - x)

= (W/2)  x + Wa - Wx - Wa + (W/2)  x

= 0

Therefore, moments of primary forces are balanced.     --------------- (ii)

Hence, the advantage of balanced primary forces and moments is proved. Now Let us examine secondary forces.

The connecting rod lengths for top and bottom pistons l_o = 2080 mm and l_b = 3040 mm.

 ∴ n  = l_o /r_o = 2080/380= 5.47

and

n  = l_b /r_b= 3040 /520 = 5.85

The secondary force because of two pistons

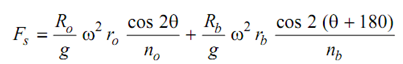
However

R_o r_o  = R_b r_b  = W

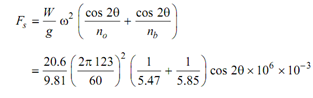
 = 2.1 × 165.9 × 0.354 × 10³  × cos 2θ

F_s  = 123.245 × 10³  cos 2θ N

(iii)

The maximum value shall occur for θ = 0 and θ = π , that is. While cranks are in horizontal or vertical plane. Apparently the resultant secondary force is the total of secondary forces because of two pistons. Therefore, there shall be moment upon the shaft.