Operation Allocation in a Cell with Negligible Setup Time

Flexibility is one of the significant features of cellular manufacturing. That is, an operation on a part might be performed on alternative machines. As a result, it may take more processing time on a machine at less operating cost, compared along with less processing time at higher operating value on another machine. Thus, for a minimum-cost production the allocations of operations shall be different than for a production plans for minimum processing time or balancing of workloads.

Production of parts has two significant criteria from the manufacturing view point, 1st minimum processing time and 2nd rapid delivery of parts. Balancing of workloads on the machines is another consideration from the cell operation viewpoint. In this section an easy mathematical programming models for operations allocations in a cell meeting these objective is specified when the setup times are negligible.

P = part types (p = 1, 2, 3, . . . , P)

d_k = demand of each part types

M = machine types (m = 1, 2, 3, . . . , M)

o_k = operations are performed on part type p.

c_m = capacity of each machine

The unit processing time & unit processing cost needed to perform an operation on a part are defined as:

Because of the flexibility of machine, an operation might be performed on alternative machines. Thus, a part has different processing routes for manufacturing.

If in a plan l the o^th operation on the p^th part is carry out on m^th machine

Let Y_pl  be the decision variable representing the number of units of part p to be processed by using plan l. The objective of minimizing the entirety processing cost to manufacture all of the parts is given by following

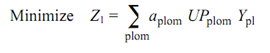
Subjected to following

(4)

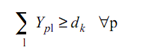
(5)

          ∑a_plom UT_plom Y_pl ≤ c_m ∀_m   

₍₆₎      

          Y_pl  > 0  ∀p, l         

Constraint 3 refers that the demand for all of parts should be met; constraint 2 refers that the capacity of machines must not be violated, & constraints 3 represent the non- negativity of the decisions variables.

Likewise, the objective of minimizing the overall processing time to manufacture all the parts is illustrated by

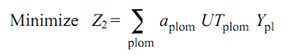
Subjected to following constraints :

Same as constraints 4, 5, 6.

The objective of balancing the workloads is specified by

Subjected to following constraints:

Similar as constraints 4, 5, 6

Solution to this kind of mathematical model might be easily found out using existing software packages as LINDO etc.