Transformation matrix:

Let us assume a general transformation matrix

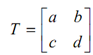
and any point A [x, y].

Then   

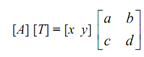
If          b = c = 0 and d = 1

then    

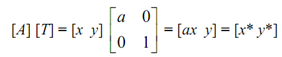
This is clear that x* generates a scale change in x component of the position vectors. Likewise, if b = c = 0 and a = 1 then

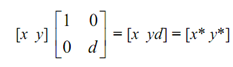
y* generates scale change in y component and if both a and d are not equal to 1 then there is scale change in both of the directions.

If a = d > 1, after that it is a case of pure enlargement.

If a = d < 1, after that it is a case of pure compression. In scaling, just the diagonal terms are affected.