Sampling from Normal Distributions:

The exact sampling distribution of a statistics can be derived in certain cases. For example the distribution of the sample mean x¯ of a random sample X of size n from a normal population follows from case (iii) under distribution of sums of random variables in Section 6.2. From that it follows that Y = 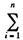X_i =n x¯, has a N (n, μ, n σ² ) distribution and thus x¯ has N (μ,σ²/n) distribution and

E(x¯) = μ, Var (x¯) = σ²/n

It can be further shown that, for samples from a normal population, x¯ and S² are independently distributed and ns²/σ² has x² _(n-1) distribution. The proof of these results is omitted.

Since

(x¯ - μ)/ (σ/√n) ∼ N (0, 1) and nS²/σ² ∼ x²_(n-1)

it follows from equation (6.10) that

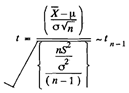
Writing s² for n S ²/ (n - 1), we have

t= X - μ/s^-/√n ∼ t _n-1

In' particular when μ = 0, the statistics t = x¯ ( s/√n) follows Student's t- distribution with ( n - 1 ) degrees of freedom. Several applications of this result will be considered in Block 3. Note that s² = n S²/( n - 1 ) and E ( s ² ) = n E ( s² )/( n-1)=σ²

If S₁² and S₂², are the sample variances of two independent random samples

X₁ = (X₁₁,X₁₂,...,X_in₁)

And

X₂ = (X₂₁,X₂₂,...,X₂n₂)

of sizes n_l and n₂, from two normal populations N ( μ_l, σ_l² ) and N ( μ₂, σ₂² ) respectively, then

n₁S₁²/σ₁² ∼ x²_n1-1

n₂S₂²/σ₂² ∼ x²_n2-1

And

 F=(n₁S₁²/(n₁-1) σ₁²)/( n₂S₂²/(n₂-1) σ₂²) -F(n₁-1,n₂-1)

Let

S₁² = n₁S₁²/(n₁-1)' s₂² = n₂S₂²/(n₂-1)

Then it follows which the statistic F = (s₁²/ σ₁²)/ (s₂²/ σ₂²) follows the F-distribution with n_l - 1and n₂ - 1 degree of freedom. Applications of all above results will be considered later.