VARIABLES
Like random variables, functions of random variables are required to be considered because they may be relevant to the problem at hand. For example, if the radius X of a manufactured pipe is a random variable then the area of the cross section of the 7 pipe which is ? X2, and is a function of X, may be also relevant to the problem under consideration. Again if ( X, Y ) implies the random coordinate of the point of hit aimed at a point target on a plane with reference to two mutually perpendicular axes passing through the target then the distance between the target and the point of hit is the function √X2+Y2 ,of the two random variables x and Y. Sometimes a function of random variables does not represent a physical quantity but is still considered in order to make meaningful statistical inference.
A function of a random variable assumes a value depending on the value that the random variable itself assumes. Let Y = G (X) be a function of a random variable X. Since X is a function defined on the sample space and Y is a function of X, so Y is a composite function defined over the sample space. Hence Y is a random variable and it is associated with a probability distribution, which depends on the probability distribution X.
More generally, if a random vector Y is defined as a function, Y = g ( X ) , of a random vector X then corresponding to the multivariate distribution of X there is a multivariate distribution of Y. The relation among a point in the sample space, a realization x of a random variable X and the corresponding realization y of the function Y = g ( X ) is illustrated Figure 1.
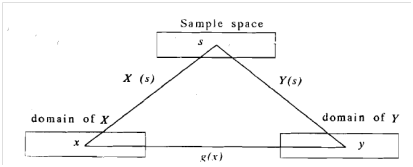
Figure 1: Relation among S , X and Y
The distribution of a function Y = g ( X ) of a random vector X may in general be difficult to determine explicitly for a given function g and a given vector X. However, the distribution may be found by one or the other of three different approaches based on derivation of the cdf, the pmf or pdf and the mgf of Y, for most cases of interest.