Inertia forces:

The inertia forces shown in Figure (d) are acting on a particle of mass dm. Out of these two; the normal inertial force dm r ω² shall be acting along the radius and will pass through O. While the tangential inertial force dm rα will be perpendicular to the radius and will cause inertial moment of the magnitude dm r ² α about O.

If we consider such inertial forces acting on the entire volume of the body, normal inertial forces will be passing through the axis of rotation while tangential inertial forces will exert a moment

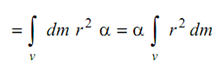
     = I α

The body rotates about an axis through O due to external action of forces which constitute a couple M.

Therefore, writing down equilibrium equation for ∑ M ₀  = 0 , we have

                                     M - I_α = 0

where   I = Moment of inertia of the body about its centroidal axis.